【題目】給出下列命題：①若
，則
；②若
，
，則
；③若，則
；④
；⑤若
，
，則，
；⑥正數(shù)
，
滿足
，則
的最小值為
．其中正確命題的序號是__________．
【答案】②③④⑤
【解析】分析：利用不等式的性質(zhì)與基本不等式對①②③④⑤⑥逐項判斷即可．
詳解：①若a＜b＜0，則
，故①錯誤；
②若a＞0，b＞0，則
≥
（當且僅當a=b時取等號）；
又﹣
=（1﹣
）≥（1﹣
）=
＞0≥0，
所以≥
，綜上，
≥≥，故②正確；
③若a＜b＜0，則a2＞ab＞0，ab＞b2＞0，
因此，a2＞ab＞b2，故③正確；
④lg9lg 11＜（
）2=
＜
=1，故④正確；
⑤若a＞b，
＞
﹣＞0
＞0
＜0，則ab＜0，所以a＞0，b＜0，故⑤正確；
⑥正數(shù)x，y滿足
+
=1，則x+2y=（x+2y）（+）=1+2+
+
≥3+2
，故其最小值為3+2
，故⑥錯誤．
綜上所述，正確命題的序號是：②③④⑤，
故答案為：②③④⑤．
閱讀快車系列答案科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)
，其中
（1）當
時，求函數(shù)
在
處的切線方程；
（2）若函數(shù)
在定義域上有且只有一個極值點，求實數(shù)
的取值范圍；
（3）若對任意
恒成立，求實數(shù)
的取值范圍.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】（本題滿分12分）已知極坐標系的極點與直角坐標系的原點重合，極軸與直角坐標系的x軸的正半軸重合，且兩個坐標系的單位長度相同．已知直線l的參數(shù)方程為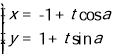
（t為參數(shù)），曲線C的極坐標方程為
．
（Ⅰ）若直線l的斜率為-1，求直線l與曲線C交點的極坐標；
（Ⅱ）若直線l與曲線C相交弦長為
，求直線l的參數(shù)方程（標準形式）．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知雙曲線
和橢圓
有公共的焦點，且離心率為
．
（Ⅰ）求雙曲線
的方程．
（Ⅱ）經(jīng)過點
作直線
交雙曲線
于
， 
兩點，且
為
的中點，求直線
的方程．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知點
在函數(shù)
的圖象上，數(shù)列
的前
項和為
，數(shù)列
的前 項和為
，且是
與
的等差中項．
（
）求數(shù)列的通項公式．
（
）設(shè)
，數(shù)列
滿足
，
．求數(shù)列的前項和
．
（
）在（）的條件下，設(shè)
是定義在正整數(shù)集上的函數(shù)，對于任意的正整數(shù)
，
，恒有
成立，且
（
為常數(shù)，
），試判斷數(shù)列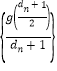
是否為等差數(shù)列，并說明理由．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】如圖,過底面是矩形的四棱錐FABCD的頂點F作EF∥AB,使AB＝2EF,且平面ABFE⊥平面ABCD,若點G在CD上且滿足DG＝G
.
求證:(1)FG∥平面AED;
(2)平面DAF⊥平面BAF.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知橢圓E: 
的左焦點為
,且過點
.
(Ⅰ)求橢圓E的方程；
(Ⅱ)設(shè)直線
與橢圓E交于
兩點，與
的交點為
，且滿足. 
①若
,求： 
的值；
②設(shè)點
是橢圓E的左頂點，點
關(guān)于
軸的對稱點為點
，試探究：在線段
上是否存在一個定點
，使得直線
過定點
，如果存在，求出點
的坐標；如果不存在，請說明理由。
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】袋中裝有大小形狀完全相同的5個小球，其中3個白球的標號分別為1、 2 、3， 2 個黑球的標號分別為1、3.
（Ⅰ）從袋中隨機摸出兩個球，求摸到的兩球顏色與標號都不相同的概率；
（Ⅱ）從袋中有放回地摸球，摸兩次，每次摸出一個球，求摸出的兩球的標號之和小于4 的概率.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
