
【題目】已知函數![]() ,其中
,其中![]()
(1)當![]() 時,求函數
時,求函數![]() 在
在![]() 處的切線方程;
處的切線方程;
(2)若函數![]() 在定義域上有且只有一個極值點,求實數
在定義域上有且只有一個極值點,求實數![]() 的取值范圍;
的取值范圍;
(3)若對任意![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1) ![]() ;(2)
;(2) ![]() ;(3)
;(3) ![]() .
.
【解析】試題分析:(1)先求![]() 切線方程
切線方程![]() (2)求導得
(2)求導得![]() ,令
,令![]() ,再分
,再分![]() 和
和![]() 三種情況討論,借助導數工具求得正解;(3)利用分類討論思想分
三種情況討論,借助導數工具求得正解;(3)利用分類討論思想分![]() 和
和![]() 三種情況討論,借助導數工具求得正解;
三種情況討論,借助導數工具求得正解;
試題解析:(1)當![]() 則
則![]()
又![]() 則切線的斜率
則切線的斜率![]() ,
,
所以函數![]() 在
在![]() 處的切線方程為
處的切線方程為![]() .
.
(2)![]() ,
, ![]() ,則
,則![]() ,
,
令![]() ,
,
①若![]() ,則
,則![]() ,故
,故![]() ,函數
,函數![]() 在
在![]() 上單調遞增,所以函數
上單調遞增,所以函數![]() 在
在![]() 上無極值點,故
上無極值點,故![]() 不符題意,舍去;
不符題意,舍去;
②若![]() ,
, ![]() ,該二次函數開口向下,對稱軸
,該二次函數開口向下,對稱軸![]() ,
, ![]() ,
,
所以![]() 在
在![]() 上有且僅有一根
上有且僅有一根![]() ,故
,故![]() ,
,
且當![]() 時,
時, ![]() ,
, ![]() ,函數
,函數![]() 在
在![]() 上單調遞增;
上單調遞增;
當![]() 時,
時, ![]() ,
, ![]() ,函數
,函數![]() 在
在![]() 上單調遞減;
上單調遞減;
所以![]() 時,函數
時,函數![]() 在定義域上有且僅有一個極值點
在定義域上有且僅有一個極值點![]() ,符合題意;
,符合題意;
③若![]() ,
, ![]() ,該二次函數開口向上,對稱軸
,該二次函數開口向上,對稱軸![]() .
.
(ⅰ)若![]() ,即
,即![]() ,
, ![]() ,故
,故![]() ,函數
,函數![]() 在
在![]() 上單調遞增,所以函數
上單調遞增,所以函數![]() 在
在![]() 上無極值點,故
上無極值點,故![]() 不符題意,舍去;
不符題意,舍去;
(ⅱ)若![]() ,即
,即![]() ,又
,又![]() ,所以方程
,所以方程![]() 在
在![]() 上有兩根
上有兩根![]() ,
, ![]() ,故
,故![]() ,且
,且
當![]() 時,
時, ![]() ,
, ![]() ,函數
,函數![]() 在
在![]() 上單調遞增;
上單調遞增;
當![]() 時,
時, ,
![]() ,函數
,函數![]() 在
在![]() 上單調遞減;
上單調遞減;
當![]() 時,
時, ![]() ,
, ![]() ,函數
,函數![]() 在
在![]() 上單調遞增;
上單調遞增;
所以函數![]() 在
在![]() 上有兩個不同的極值點,故
上有兩個不同的極值點,故![]() 不符題意,舍去,
不符題意,舍去,
綜上所述,實數![]() 的取值范圍是
的取值范圍是![]() .
.
(3)由(2)可知,
①當![]() 時,函數
時,函數![]() 在
在![]() 上單調遞增,所以當
上單調遞增,所以當![]() 時,
時,
![]() ,符合題意,
,符合題意,
②當![]() 時,
時, ![]() ,
,
(ⅰ)若![]() ,即
,即![]() ,函數
,函數![]() 在
在![]() 上單調遞減,故
上單調遞減,故![]() ,不符題意,舍去,
,不符題意,舍去,
(ⅱ)若![]() ,即
,即![]() ,故函數
,故函數![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減,
上單調遞減,
當![]() 時,
時, ![]() (事實上,令
(事實上,令![]() ,
, ![]() ,則
,則![]() ,函數
,函數![]() 在
在![]() 上單調遞減,所以
上單調遞減,所以![]() ,即
,即![]() 對任意
對任意![]() 恒成立.)
恒成立.)
所以存在![]() ,使得
,使得![]() ,故
,故![]() 不符題意,舍去;
不符題意,舍去;
③當![]() 時,
時, ![]() ,函數
,函數![]() 在
在![]() 上單調遞增,所以當
上單調遞增,所以當![]() 時,
時, ![]() ,符合題意.
,符合題意.
綜上所述,實數![]() 的取值范圍是
的取值范圍是![]() .
.


 課時訓練江蘇人民出版社系列答案
課時訓練江蘇人民出版社系列答案 黃岡經典趣味課堂系列答案
黃岡經典趣味課堂系列答案 啟東小題作業本系列答案
啟東小題作業本系列答案科目:高中數學 來源: 題型:
【題目】已知數列{an}中,a1=3,a10=21,通項an相應的函數是一次函數.
(1) 求數列{an}的通項公式;
(2) 若{bn}是由a2,a4,a6,a8,…組成,試求數列{bn}的通項公式.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】判斷下列集合間的關系:
(1)A={x|x-3>2},B={x|2x-5≥0};
(2)A={x∈Z|-1≤x<3},B={x|x=|y|,y∈A}.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系中,以坐標原點為極點,![]() 軸的非負半軸為極軸建立極坐標系,已知曲線
軸的非負半軸為極軸建立極坐標系,已知曲線![]() 的極坐標方程為
的極坐標方程為![]() ,它在點
,它在點![]() 處的切線為直線
處的切線為直線![]() .
.
(Ⅰ)求直線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)已知點![]() 為橢圓
為橢圓![]() 上一點,求點
上一點,求點![]() 到直線
到直線![]() 的距離的取值范圍.
的距離的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,BC邊上的高所在的直線方程為x-2y+1=0,∠A的平分線所在的直線方程為y=0. 若B的坐標為(1,2),求△ABC三邊所在直線方程及點C坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,拋物線![]() 的焦點為
的焦點為![]() ,拋物線上一定點
,拋物線上一定點![]() .
.
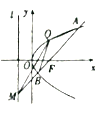
(1)求拋物線![]() 的方程及準線
的方程及準線![]() 的方程;
的方程;
(2)過焦點![]() 的直線(不經過
的直線(不經過![]() 點)與拋物線交于
點)與拋物線交于![]() 兩點,與準線
兩點,與準線![]() 交于點
交于點![]() ,記
,記![]() 的斜率分別為
的斜率分別為![]() ,問是否存在常數
,問是否存在常數![]() ,使得
,使得![]() 成立?若存在
成立?若存在![]() ,求出
,求出![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】
周銷售量(單位:噸) | 2 | 3 | 4 |
頻數 | 20 | 50 | 30 |
⑴ 根據上面統計結果,求周銷售量分別為2噸,3噸和4噸的頻率;
⑵ 已知每噸該商品的銷售利潤為2千元,![]() 表示該種商品兩周銷售利潤的和(單位:千元),若以上述頻率作為概率,且各周的銷售量相互獨立,求
表示該種商品兩周銷售利潤的和(單位:千元),若以上述頻率作為概率,且各周的銷售量相互獨立,求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com