
 如圖,四棱錐B-ACDE的底面ACDE滿足 DE∥AC,AC=2DE.
如圖,四棱錐B-ACDE的底面ACDE滿足 DE∥AC,AC=2DE.分析 用分析法證明第(Ⅰ)問,用反證法證明第 (Ⅱ)問,根據分析法、反證法的證明步驟,即可得出結論.
解答 (Ⅰ)證明:欲證平面ABE⊥平面BCD,
只需證AB⊥平面BCD,----------------------------------------------(2分)
由已知AB⊥BC,只需證AB⊥DC,-------------------------------------------------(4分)
由已知DC⊥平面ABC可得DC⊥AB成立,
所以平面ABE⊥平面BCD.
(Ⅱ)證明:假設在平面ABE內存在直線與DC平行,---------------------------------(6分)
又因為DC?平面ABE,所以DC∥平面ABE.
又因為平面ACDE∩平面ABE=AE,
所以DC∥AE,---------------------------------------(8分)
又因為DE∥AC,所以ACDE是平行四邊形,
所以AC=DE,這與AC=2DE矛盾,---------------------------------------------(10分)
所以假設錯誤,原結論正確.
故答案為AB⊥平面BCD;AB⊥DC;在平面ABE內存在直線與DC平行;DC∥AE;AC=2DE.
點評 本題考查分析法、反證法,考查學生分析解決問題的能力,正確運用分析法、反證法是關鍵.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
| P(K2≥k0) | 0.10 | 0.05 | 0.010 |
| k0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 0 | B. | $\frac{3}{2}$ | C. | $\frac{3}{4}$ | D. | 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
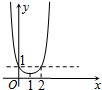
| A. | (-∞,0) | B. | (2,+∞) | C. | (0,1) | D. | (0,2) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com