Question

1．已知A（1，1），B（-2，3），O為坐標原點，若直線l：ax+by+1=0與△ABO所圍成的區域（包括邊界）沒有公共點，則a-3b的取值范圍為（-∞，$\frac{7}{5}$）．

Answer 1

分析 根據所給的三個點的坐標和直線與△ABO所圍成的區域（包括邊界）沒有公共點，得到關于a，b的不等式組，根據不等式組畫出可行域，求出目標函數的取值范圍．

解答 解：A（1，1），B（-2，3），O為坐標原點，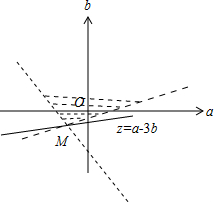
直線l：ax+by+1=0與△ABO所圍成區域（包含邊界）
沒有公共點，
得不等式組$\left\{\begin{array}{l}{a+b+1＞0}\\{-2a+3b+1＞0}\end{array}\right.$，
令z=a-3b，
畫出不等式組表示的平面區域，
判斷知，z=a-3b在A取得最大值，
由$\left\{\begin{array}{l}{a+b+1=0}\\{-2a+3b+1=0}\end{array}\right.$，解得M（-$\frac{2}{5}$，-$\frac{3}{5}$），
可得a-3b＜$\frac{7}{5}$．
∴a-3b的取值范圍是（-∞，$\frac{7}{5}$）．
故答案為：（-∞，$\frac{7}{5}$）．

點評 本題考查線性規劃的應用，本題解題的關鍵是寫出約束條件，表示出目標函數，畫出可行域，得到最優解，是中檔題．