
【題目】已知函數f(x)=![]() 是定義在R上的奇函數;
是定義在R上的奇函數;
(1)求a、b的值,判斷并證明函數y=f(x)在區間(1,+∞)上的單調性
(2)已知k<0且不等式f(t2-2t+3)+f(k-1)<0對任意的t∈R恒成立,求實數k的取值范圍.
【答案】(1)見解析(2)(-1,0)
【解析】
(1)根據奇函數的定義即可求出a、b的值,再根據增減性定義證明函數單調性即可
(2)根據奇函數的性質及函數的增減性原不等式可轉化為t2-2t+3>1-k對任意的t∈R恒成立,只需求出t2-2t+3的最小值即可.
(1)∵函數f(x)=![]() 是奇函數
是奇函數
∴由定義f(-x)=![]() =-
=-![]() ,
,
∴a=b=0,
∴f(x)=![]() ,
,
y=f(x)在區間(1,+∞)上的單調遞減.
證明如下:
∵f(x)=![]() ,∴
,∴![]() ,
,
∵x>1,∴![]() ,
,
∴y=f(x)在區間(1,+∞)上的單調遞減.
(2)由f(t2-2t+3)+f(k-1)<0及f(x)為奇函數得:f(t2-2t+3)<f(1-k)
因為t2-2t+3≥2,1-k>1,且y=f(x)在區間(1,+∞)上的單調遞減,
所以t2-2t+3>1-k任意的t∈R恒成立,
因為t2-2t+3的最小值為2,所以2>1-k,∴k>-1
∵k<0,∴-1<k<0.
∴實數k的取值范圍是(-1,0).


 天天向上口算本系列答案
天天向上口算本系列答案科目:高中數學 來源: 題型:
【題目】在籃球比賽中,如果某位球員的得分,籃板,助攻,搶斷,蓋帽中有兩個值達到![]() 或
或![]() 以上,就稱該球員拿到了兩雙.下表是某球員在最近五場比賽中的數據統計:
以上,就稱該球員拿到了兩雙.下表是某球員在最近五場比賽中的數據統計:
場次 | 得分 | 籃板 | 助攻 | 搶斷 | 蓋帽 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(![]() )從上述比賽中任選
)從上述比賽中任選![]() 場,求該球員拿到“兩雙”的概率.
場,求該球員拿到“兩雙”的概率.
(![]() )從上述比賽中任選
)從上述比賽中任選![]() 場,設該球員拿到“兩雙”的次數為
場,設該球員拿到“兩雙”的次數為![]() ,求
,求![]() 的分布列及數學期望.
的分布列及數學期望.
(![]() )假設各場比賽互相獨立,將該球員在上述比賽中獲得“兩雙”的頻率作為概率,設其在接下來的三場比賽中獲得“兩雙”的次數為
)假設各場比賽互相獨立,將該球員在上述比賽中獲得“兩雙”的頻率作為概率,設其在接下來的三場比賽中獲得“兩雙”的次數為![]() ,試比賽
,試比賽![]() 與
與![]() 的大小關系(只需寫出結論).
的大小關系(只需寫出結論).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在極坐標系中,已知圓C的圓心C( ![]() ,
, ![]() ),半徑r=
),半徑r= ![]() .
.
(1)求圓C的極坐標方程;
(2)若α∈[0, ![]() ),直線l的參數方程為
),直線l的參數方程為 ![]() (t為參數),直線l交圓C于A、B兩點,求弦長|AB|的取值范圍.
(t為參數),直線l交圓C于A、B兩點,求弦長|AB|的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數g(x)=ax2-2ax+1+b(a>0)在區間[2,4]上的最大值為9,最小值為1,記f(x)=g(|x|).
(1)求實數a,b的值;
(2)若不等式f(log2k)>f(2)成立,求實數k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某大學進行自主招生時,需要進行邏輯思維和閱讀表達兩項能力的測試.學校對參加測試的200名學生的邏輯思維成績、閱讀表達成績以及這兩項的總成績進行了排名.其中甲、乙、丙三位同學的排名情況如下圖所示:
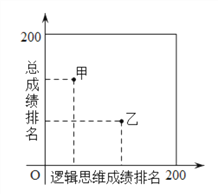

得出下面四個結論:
①甲同學的閱讀表達成績排名比他的邏輯思維成績排名更靠前
②乙同學的邏輯思維成績排名比他的閱讀表達成績排名更靠前
③甲、乙、丙三位同學的邏輯思維成績排名中,甲同學更靠前
④乙同學的總成績排名比丙同學的總成績排名更靠前
則所有正確結論的序號是_________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合A={x|1≤x≤3},B={x|x>2}.
(Ⅰ)分別求A∩B,(RB)∪A;
(Ⅱ)已知集合C={x|1<x<a},若CA,求實數a的取值集合.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|x﹣1|+|x+a|,其中a為實常數.
(1)若函數f(x)的最小值為2,求a的值;
(2)當x∈[0,1]時,不等式|x﹣2|≥f(x)恒成立,求a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com