
【題目】A地的天氣預報顯示,A地在今后的三天中,每一天有強濃霧的概率為![]() ,現用隨機模擬的方法估計這三天中至少有兩天有強濃霧的概率,先利用計算器產生
,現用隨機模擬的方法估計這三天中至少有兩天有強濃霧的概率,先利用計算器產生![]() 之間整數值的隨機數,并用0,1,2,3,4,5,6表示沒有強濃霧,用7,8,9表示有強濃霧,再以每3個隨機數作為一組,代表三天的天氣情況,產生了如下20組隨機數:
之間整數值的隨機數,并用0,1,2,3,4,5,6表示沒有強濃霧,用7,8,9表示有強濃霧,再以每3個隨機數作為一組,代表三天的天氣情況,產生了如下20組隨機數:
402 978 191 925 273 842 812 479 569 683
231 357 394 027 506 588 730 113 537 779
則這三天中至少有兩天有強濃霧的概率近似為![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:高中數學 來源: 題型:
【題目】定義域是![]() 上的連續函數
上的連續函數![]() 圖像的兩個端點為
圖像的兩個端點為![]() 、
、![]() ,
,![]() 是圖像
是圖像![]() 上任意一點,過點
上任意一點,過點![]() 作垂直于
作垂直于![]() 軸的直線
軸的直線![]() 交線段
交線段![]() 于點
于點![]() (點
(點![]() 與點
與點![]() 可以重合),我們稱
可以重合),我們稱![]() 的最大值為該函數的“曲徑”,下列定義域是
的最大值為該函數的“曲徑”,下列定義域是![]() 上的函數中,曲徑最小的是( )
上的函數中,曲徑最小的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
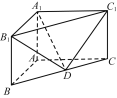
【題目】在直三棱柱ABC-A1B1C1中,已知AB⊥AC,AB=2,AC=4,AA1=3,D是BC的中點.
(1) 求直線DC1與平面A1B1D所成角的正弦值;
(2) 求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地實行垃圾分類后,政府決定為![]() 三個小區建造一座垃圾處理站M,集中處理三個小區的濕垃圾.已知
三個小區建造一座垃圾處理站M,集中處理三個小區的濕垃圾.已知![]() 在
在![]() 的正西方向,
的正西方向,![]() 在
在![]() 的北偏東
的北偏東![]() 方向,
方向,![]() 在
在![]() 的北偏西
的北偏西![]() 方向,且在
方向,且在![]() 的北偏西
的北偏西![]() 方向,小區
方向,小區![]() 與
與![]() 相距
相距![]() 與
與![]() 相距
相距![]() .
.
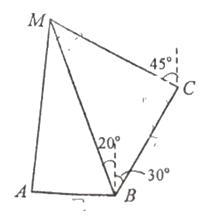
(1)求垃圾處理站![]() 與小區
與小區![]() 之間的距離;
之間的距離;
(2)假設有大、小兩種運輸車,車在往返各小區、處理站之間都是直線行駛,一輛大車的行車費用為每公里![]() 元,一輛小車的行車費用為每公里
元,一輛小車的行車費用為每公里![]() 元(其中
元(其中![]() 為滿足
為滿足![]() 是
是![]() 內的正整數) .現有兩種運輸濕垃圾的方案:
內的正整數) .現有兩種運輸濕垃圾的方案:
方案1:只用一輛大車運輸,從![]() 出發,依次經
出發,依次經![]() 再由
再由![]() 返回到
返回到![]() ;
;
方案2:先用兩輛小車分別從![]() 運送到
運送到![]() ,然后并各自返回到
,然后并各自返回到![]() ,一輛大車從
,一輛大車從![]() 直接到
直接到![]() 再返回到
再返回到![]() .試比較哪種方案更合算?請說明理由. 結果精確到小數點后兩位
.試比較哪種方案更合算?請說明理由. 結果精確到小數點后兩位
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年來,隨著![]() 網絡的普及和智能手機的更新換代,各種方便的
網絡的普及和智能手機的更新換代,各種方便的![]() 相繼出世,其功能也是五花八門.某大學為了調查在校大學生使用
相繼出世,其功能也是五花八門.某大學為了調查在校大學生使用![]() 的主要用途,隨機抽取了
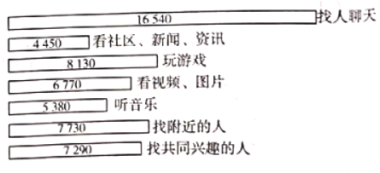
的主要用途,隨機抽取了![]() 名大學生進行調查,各主要用途與對應人數的結果統計如圖所示,現有如下說法:
名大學生進行調查,各主要用途與對應人數的結果統計如圖所示,現有如下說法:
①可以估計使用![]() 主要聽音樂的大學生人數多于主要看社區、新聞、資訊的大學生人數;
主要聽音樂的大學生人數多于主要看社區、新聞、資訊的大學生人數;
②可以估計不足![]() 的大學生使用
的大學生使用![]() 主要玩游戲;
主要玩游戲;
③可以估計使用![]() 主要找人聊天的大學生超過總數的
主要找人聊天的大學生超過總數的![]() .
.
其中正確的個數為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,將![]() 方格紙中每個小方格染三種顏色之一,使得每種顏色的小方格的個數相等.若相鄰兩個小方格的顏色不同,稱他們的公共邊為“分割邊”,則分割邊條數的最小值為( )
方格紙中每個小方格染三種顏色之一,使得每種顏色的小方格的個數相等.若相鄰兩個小方格的顏色不同,稱他們的公共邊為“分割邊”,則分割邊條數的最小值為( )

A.33B.56C.64D.78
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】分形幾何是美籍法國數學家芒德勃羅在20世紀70年代創立的一門數學新分支,其中的“謝爾賓斯基”圖形的作法是:先作一個正三角形,挖去一個“中心三角形”(即以原三角形各邊的中點為頂點的三角形),然后在剩下的每個小正三角形中又挖去一個“中心三角形”.按上述方法無限連續地作下去直到無窮,最終所得的極限圖形稱為“謝爾賓斯基”圖形(如圖所示),按上述操作7次后,“謝爾賓斯基”圖形中的小正三角形的個數為( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數據![]() 是鄭州市普通職工
是鄭州市普通職工![]() 個人的年收入,若這
個人的年收入,若這![]() 個數據的中位數為
個數據的中位數為![]() ,平均數為
,平均數為![]() ,方差為
,方差為![]() ,如果再加上世界首富的年收入
,如果再加上世界首富的年收入![]() ,則這
,則這![]() 個數據中,下列說法正確的是( )
個數據中,下列說法正確的是( )
A.年收入平均數大大增大,中位數一定變大,方差可能不變
B.年收入平均數大大增大,中位數可能不變,方差變大
C.年收入平均數大大增大,中位數可能不變,方差也不變
D.年收入平均數可能不變,中位數可能不變,方差可能不變
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義:對于一個項數為![]() 的數列
的數列![]() ,若存在
,若存在![]() 且
且![]() ,使得數列
,使得數列![]() 的前k項和與剩下項的和相等(若僅為1項,則和為該項本身),我們稱該數列是“等和數列”.例如:因為
的前k項和與剩下項的和相等(若僅為1項,則和為該項本身),我們稱該數列是“等和數列”.例如:因為![]() ,所以數列3,2,1是“等和數列”.請解答以下問題:
,所以數列3,2,1是“等和數列”.請解答以下問題:
(1)數列1,2,p,4是“等和數列”,求實數p的值;
(2)項數為![]() 的等差數列
的等差數列![]() 的前n項和為
的前n項和為![]() ,
,![]() ,求證:
,求證:![]() 是“等和數列”.
是“等和數列”.
(3)![]() 是公比為q項數為
是公比為q項數為![]() 的等比數列
的等比數列![]() ,其中
,其中![]() 且
且![]() 恒成立.判斷
恒成立.判斷![]() 是不是“等和數列”,并證明你的結論.
是不是“等和數列”,并證明你的結論.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com