
【題目】近年來,隨著![]() 網絡的普及和智能手機的更新換代,各種方便的
網絡的普及和智能手機的更新換代,各種方便的![]() 相繼出世,其功能也是五花八門.某大學為了調查在校大學生使用
相繼出世,其功能也是五花八門.某大學為了調查在校大學生使用![]() 的主要用途,隨機抽取了
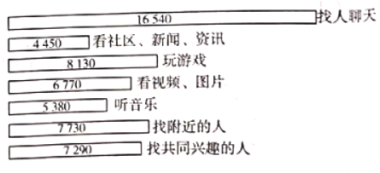
的主要用途,隨機抽取了![]() 名大學生進行調查,各主要用途與對應人數的結果統計如圖所示,現有如下說法:
名大學生進行調查,各主要用途與對應人數的結果統計如圖所示,現有如下說法:
①可以估計使用![]() 主要聽音樂的大學生人數多于主要看社區、新聞、資訊的大學生人數;
主要聽音樂的大學生人數多于主要看社區、新聞、資訊的大學生人數;
②可以估計不足![]() 的大學生使用
的大學生使用![]() 主要玩游戲;
主要玩游戲;
③可以估計使用![]() 主要找人聊天的大學生超過總數的
主要找人聊天的大學生超過總數的![]() .
.
其中正確的個數為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 全能測控一本好卷系列答案
全能測控一本好卷系列答案科目:高中數學 來源: 題型:
【題目】已知函數![]()
![]() 常數
常數![]() )滿足
)滿足![]() .
.
(1)求出![]() 的值,并就常數
的值,并就常數![]() 的不同取值討論函數
的不同取值討論函數![]() 奇偶性;
奇偶性;
(2)若![]() 在區間
在區間![]() 上單調遞減,求
上單調遞減,求![]() 的最小值;
的最小值;
(3)在(2)的條件下,當![]() 取最小值時,證明:
取最小值時,證明:![]() 恰有一個零點
恰有一個零點![]() 且存在遞增的正整數數列
且存在遞增的正整數數列![]() ,使得
,使得![]() 成立.
成立.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司租賃甲、乙兩種設備生產A,B兩類產品,甲種設備每天能生產A類產品5件和B類產品10件,乙種設備每天能生產A類產品6件和B類產品20件.已知設備甲每天的租賃費為200元,設備乙每天的租賃費為300元,現該公司至少要生產A類產品50件,B類產品140件,所需租賃費最少為__________元.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ex+e-x,其中e是自然對數的底數.
(1)證明:f(x)是R上的偶函數;
(2)若關于x的不等式mf(x)≤e-x+m-1在(0,+∞)上恒成立,求實數m的取值范圍;
(3)已知正數a滿足:存在x0∈[1,+∞),使得f(x0)<a(-![]() +3x0)成立.試比較ea-1與ae-1的大小,并證明你的結論.
+3x0)成立.試比較ea-1與ae-1的大小,并證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).以原點
為參數).以原點![]() 為極點,
為極點,![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,且直線
,且直線![]() 與曲線
與曲線![]() 交于
交于![]() 、
、![]() 兩點.
兩點.
(1)求實數![]() 的取值范圍;
的取值范圍;
(2)若![]() ,點
,點![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
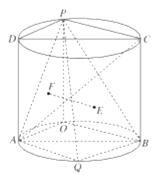
【題目】如圖,圓柱的軸截面![]() 是邊長為2的正方形,點P是圓弧
是邊長為2的正方形,點P是圓弧![]() 上的一動點(不與
上的一動點(不與![]() 重合),點Q是圓弧
重合),點Q是圓弧![]() 的中點,且點
的中點,且點![]() 在平面
在平面![]() 的兩側.
的兩側.
(1)證明:平面![]() 平面
平面![]() ;
;
(2)設點P在平面![]() 上的射影為點O,點
上的射影為點O,點![]() 分別是
分別是![]() 和
和![]() 的重心,當三棱錐
的重心,當三棱錐![]() 體積最大時,回答下列問題.
體積最大時,回答下列問題.
(i)證明:![]() 平面
平面![]() ;
;
(ii)求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法正確的是( )
A.在頻率分布直方圖中,眾數左邊和右邊的直方圖的面積相等;
B.為調查高三年級的240名學生完成作業所需的時間,由教務處對高三年級的學生進行編號,從001到240抽取學號最后一位為3的學生進行調查,則這種抽樣方法為分層抽樣;
C.“![]() ”是“
”是“![]() ”的必要不充分條件;
”的必要不充分條件;
D.命題![]() :“
:“![]() ,使得
,使得![]() ”的否定為:“
”的否定為:“![]() ,均有
,均有![]() ”.
”.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com