【題目】如圖，在四棱錐
中，底面
是直角梯形， 
， 
， 
， 
， 
平面
， 
.
（1）求證： 
平面
；
（2）求證： 
平面
；
（3）若
是
的中點，求三棱錐
的體積.
【答案】（1）詳見解析；（2）詳見解析；（3）
.
【解析】試題分析：（1）根據線面平行的判定，只需證明直線
與平面
上的某一條直線平行即可，而條件中直接給出了
，因此結合線面平行的判定，可直接證明
平面；（2）首先根據條件中給出的數據易得
，從而根據勾股定理可得
，再由條件
平面
可得
，從而根據線面垂直的判定即可證得
平面
；（3）由
是
即可得到面
的距離是
到面距離的一半，從而
.
試題解析：（1）∵，且
平面，
平面，∴平面； 4分
（2）在直角梯形中，過
作
于點
，則四邊形
為矩形，
∴
，又∵
，∴
，在
中，
，
∴
，
，∴
，則
，
∴
，∴， 8分
又∵平面，∴
，
，∴平面； 10分
（3）∵是中點，∴到面的距離是到面距離的一半，
∴. 14分
科目：高中數學 來源： 題型：
【題目】響應“文化強國建設”號召，某市把社區圖書閱覽室建設增列為重要的民生工程.為了解市民閱讀需求，隨機抽取市民200人做調查，統計顯示，男士喜歡閱讀古典文學的有64人，不喜歡的有56人；女士喜歡閱讀古典文學的有36人，不喜歡的有44人.
（1）能否在犯錯誤的概率不超過0.25的前提下認為喜歡閱讀古典文學與性別有關系？
（2）為引導市民積極參與閱讀，有關部門牽頭舉辦市讀書交流會，從這200人中篩選出5名男代表和4名代表，其中有3名男代表和2名女代表喜歡古典文學.現從這9名代表中任選3名男代表和2名女代表參加交流會，記
為參加交流會的5人中喜歡古典文學的人數，求的分布列及數學期望
．
附：
，其中
．
參考數據：
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（附加題，本小題滿分10分，該題計入總分）
已知函數
，若在區間
內有且僅有一個
，使得
成立，則稱函數
具有性質
．
（1）若
，判斷是否具有性質，說明理由；
（2）若函數
具有性質，試求實數
的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
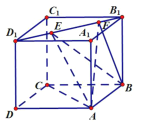
【題目】如圖所示，正方體
的棱長為1，線段
上有兩個動點
，且
，則下列結論中正確的是__________．
①
平面
；
②平面
平面
；
③三棱錐
的體積為定值；
④存在某個位置使得異面直線
與
成角
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的右焦點為
，點
在橢圓
上.
（1）求橢圓
的標準方程；
（2）是否存在斜率為
的直線
與橢圓
相交于
兩點，使得
是橢圓的左焦點
？若存在，求出直線
的方程；若不存在，說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知圓
滿足：①圓心在第一象限，截
軸所得弦長為2；②被
軸分成兩段圓弧，其弧長的比為
；③圓心到直線
的距離為
.
（Ⅰ）求圓
的方程；
（Ⅱ）若點
是直線
上的動點，過點
分別做圓
的兩條切線，切點分別為
， 
，求證：直線
過定點.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知拋物線C經過點(3,6)且焦點在x軸上．
(1)求拋物線C的標準方程；
(2)直線l： 
過拋物線C的焦點F且與拋物線C交于A，B兩點，求A，B兩點間的距離．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在直三棱柱ABC-A1B1C1中，AC=BC=CC1，AC⊥BC，點D是AB的中點．
（1）求證：CD⊥平面A1ABB1；
（2）求證：AC1∥平面CDB1．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
