
分析 (Ⅰ)根據二次函數的性質求出函數在(-4,1)的值域即可;
(Ⅱ)通過討論k的范圍,集合二次函數的性質,確定k的范圍即可;
(Ⅲ)通過討論k的范圍,判斷函數的單調性,從而確定k的范圍即可.
解答 解:(Ⅰ)當k=4時,f(x)=2x2+8x-3=2(x+2)2-11,
f(x)的對稱軸是x=-2,f(x)在(-4,-2)遞減,在(-2,1)遞增,
所以f(x)min=f(2)=-11,f(x)max=f(1)=7,
所以f(x)的值域為[-11,7)-----------------------(3分)
(Ⅱ)若函數f(x)在(0,+∞)上至少有一個零點,可分為以下三種情況:
①若k-2>0即k>2時,f(x)=(k-2)x2+2kx-3的對稱軸方程為$x=\frac{k}{2-k}<0$,
又f(0)=-3<0,由圖象可知f(x)在(0,+∞)上必有一個零點;----------------------(4分)
②若k-2=0即k=2時,f(x)=4x-3,令f(x)=0得$x=\frac{3}{4}>0$,
知f(x)在(0,+∞)上必有一個零點$\frac{3}{4}$;----------------------(5分)
③若k-2<0即k<2時,要使函數f(x)在(0,+∞)上至少有一個零點,
則需要滿足$\left\{{\begin{array}{l}{x=\frac{2k}{2-k}>0}\\{△=4{k^2}+12(k-2)≥0}\end{array}}\right.$解得$\left\{{\begin{array}{l}{0<k<2}\\{k≥\frac{{-3+\sqrt{33}}}{2}或k≤\frac{{-3-\sqrt{33}}}{2}}\end{array}}\right.$,
所以$\frac{{-3+\sqrt{33}}}{2}≤k<2$--------------------(7分)
綜上可知,若函數f(x)在(0,+∞)上至少有一個零點,k的取值范圍為$[\frac{{-3+\sqrt{33}}}{2},+∞)$----------------------(8分)
( III)①當k=2時,f(x)=4x-3在區間[1,2]上單增,所以k=2成立;-------(9分)
②當k>2時,∵f(0)=-3<0,顯然在f(x)在區間[1,2]上單增,所以k>2也成立;
--------------------(10分)
③當k<2時,∵f(0)=-3,∴必有$\frac{k}{2-k}≥2$成立,解得$\frac{4}{3}≤k<2$.---------------(11分)
綜上k的取值范圍為$[\frac{4}{3},+∞)$----------------------(12分)
點評 本題考查了函數的單調性、最值問題,考查二次函數的性質以及分類討論思想,是一道中檔題.


科目:高中數學 來源: 題型:解答題
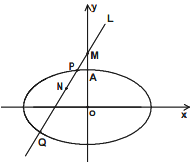 如圖,已知橢圓的中心在坐標原點,焦點在x軸上,它的一個頂點為A(0,$\sqrt{2}$),且離心率等于$\frac{{\sqrt{3}}}{2}$,過點M(0,2)的直線l與橢圓相交于不同兩點P,Q,點N在線段PQ上.
如圖,已知橢圓的中心在坐標原點,焦點在x軸上,它的一個頂點為A(0,$\sqrt{2}$),且離心率等于$\frac{{\sqrt{3}}}{2}$,過點M(0,2)的直線l與橢圓相交于不同兩點P,Q,點N在線段PQ上.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (0,+∞) | B. | (0,$\frac{1}{2}$)∪(2,+∞) | C. | (0,$\frac{1}{8}$)∪($\frac{1}{2}$,2) | D. | (0,$\frac{1}{2}$) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{2}{5}\sqrt{5}$ | B. | $\frac{{\sqrt{5}}}{2}$ | C. | $\frac{4}{5}\sqrt{5}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 求1+2+3+…+10的和 | B. | 解方程組$\left\{\begin{array}{l}{x+y+5=0}\\{x-y+3=0}\end{array}\right.$ | ||
| C. | 求半徑為3的圓的面積 | D. | 判斷y=x2在R上的單調性 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (7,-6) | B. | (7,6) | C. | (6,7) | D. | (-7,6) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 宏利重工有限公司從2012年起,若不改善生產環境,按現狀生產,每月收入為70萬元,同時將受到環保部門的處罰,第一個月罰3萬元,以后每月遞增2萬元的處罰.如果從2012年一月起投資400萬元增加回收凈化設備以改善生產環境(改造設備時間不計).按測算,新設備投產后的月收入與時間的關系如圖所示.
宏利重工有限公司從2012年起,若不改善生產環境,按現狀生產,每月收入為70萬元,同時將受到環保部門的處罰,第一個月罰3萬元,以后每月遞增2萬元的處罰.如果從2012年一月起投資400萬元增加回收凈化設備以改善生產環境(改造設備時間不計).按測算,新設備投產后的月收入與時間的關系如圖所示.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com