
分析 由題意可得f(x)min=f(x0),g(x)min=g(x0),利用基本不等式求出g(x)的最小值,得到x0=2,f(x0)=g(x0)=1,再由f(2)=1得到一個關于b,c的方程,由f'(2)=0求導b值,進一步得到c值,則函數f(x)的解析式可求,求出f(1)和 f(4)的值得答案.
解答 解:由題可知,f(x)min=f(x0),g(x)min=g(x0)------------------------(1分)
$g(x)=\frac{1}{4}x+\frac{1}{x}≥2\sqrt{\frac{1}{4}x•\frac{1}{x}}=1$-----------------------------------------------------------(2分)
當且僅當$\frac{1}{4}x=\frac{1}{x}$且1≤x≤4即x=2時取“=”,
∴x0=2,f(x0)=g(x0)=1---------------------------------------------------------(4分)
由f(2)=1,得$\frac{1}{2}•{2^2}+\frac{b}{2}+c=1$,即$1+\frac{b}{2}+c=0$---------(1)
f(x)min=f(2)=1,得x=2是f(x)的一個極值點,
∴f'(2)=0------------(6分)
$f'(x)=x-\frac{b}{x^2}$,得$f'(2)=2-\frac{b}{2^2}=2-\frac{b}{4}=0$,
∴b=8-----------------------------------------------------------------------------------------------(8分)
代入(1),得c=-5------------------------------------------------------------------------------(9分)
∴$f(x)=\frac{1}{2}{x^2}+\frac{8}{x}-5$,(1≤x≤4)-----------------------------------------------------(10分)
f(x)max=Max{f(1),f(4)},
∴$f(1)=\frac{1}{2}•{1^2}+\frac{8}{1}-5=\frac{7}{2}$<$f(4)=\frac{1}{2}•{4^2}+\frac{8}{4}-5=5$.
故f(x)的最大值是5-------------------------------------------------------------------------------(12分)
點評 本題考查利用導數研究函數的單調性,考查了利用導數求函數的最值,考查數學轉化思想方法,是中檔題.


 口算心算速算應用題系列答案
口算心算速算應用題系列答案 同步拓展閱讀系列答案
同步拓展閱讀系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-∞,0) | B. | (-1,2) | C. | (1,2) | D. | (1,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
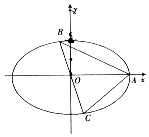 如圖,在平面直角坐標xOy中,橢圓M:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)經過點(${\sqrt{3}$,$\frac{1}{2}}$),且與圓x2+(y-3)2=4外切,過原點O的直線l的傾斜角為鈍角,且直線l交橢圓M于B,C兩點,A為橢圓的右頂點.
如圖,在平面直角坐標xOy中,橢圓M:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)經過點(${\sqrt{3}$,$\frac{1}{2}}$),且與圓x2+(y-3)2=4外切,過原點O的直線l的傾斜角為鈍角,且直線l交橢圓M于B,C兩點,A為橢圓的右頂點.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
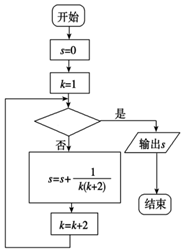
| A. | k>8? | B. | k≥9? | C. | k≥10? | D. | k>11? |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com