
 已知定點A、B間的距離為2,以B為圓心作半徑為2
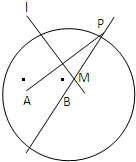
已知定點A、B間的距離為2,以B為圓心作半徑為2 的圓,P為圓上一點,線段AP的垂直平分線l與直線PB交于點M,當P在圓周上運動時,點M的軌跡記為曲線C.
的圓,P為圓上一點,線段AP的垂直平分線l與直線PB交于點M,當P在圓周上運動時,點M的軌跡記為曲線C. ,
, .
. 的橢圓,
的橢圓, ,顯然結論成立.
,顯然結論成立. ,
,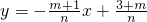 .
.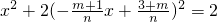 ,
,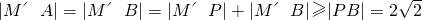
 ,所以|MB|+|MA|=2
,所以|MB|+|MA|=2 .由此能求出曲線C的方程.
.由此能求出曲線C的方程.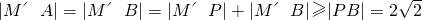 ,由此能夠證明直線l與曲線C相切.
,由此能夠證明直線l與曲線C相切.

科目:高中數學 來源: 題型:
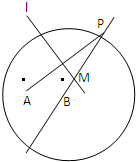 已知定點A、B間的距離為2,以B為圓心作半徑為2
已知定點A、B間的距離為2,以B為圓心作半徑為2| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
(本小題滿分15分)
已知定點A、B間的距離為2,以B為圓心作半徑為2![]() 的圓,P為圓上一點,線段AP的垂直平分線l與直線PB交于點M,當P在圓周上運動時,點M的軌跡記為曲線C.
的圓,P為圓上一點,線段AP的垂直平分線l與直線PB交于點M,當P在圓周上運動時,點M的軌跡記為曲線C.
(1)建立適當的坐標系,求曲線C的方程,并說明它是什么樣的曲線;
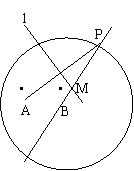 (2)試判斷l與曲線C的位置關系,并加以證明.
(2)試判斷l與曲線C的位置關系,并加以證明.
查看答案和解析>>
科目:高中數學 來源:2010-2011學年底江蘇省連云港市贛榆高級中學高三(下)摸底數學試卷(解析版) 題型:解答題
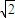 的圓,P為圓上一點,線段AP的垂直平分線l與直線PB交于點M,當P在圓周上運動時,點M的軌跡記為曲線C.
的圓,P為圓上一點,線段AP的垂直平分線l與直線PB交于點M,當P在圓周上運動時,點M的軌跡記為曲線C.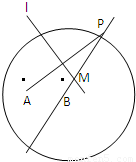
查看答案和解析>>
科目:高中數學 來源:2010-2011學年江蘇省連云港市贛榆高級中學高三(下)摸底數學試卷(解析版) 題型:解答題
 的圓,P為圓上一點,線段AP的垂直平分線l與直線PB交于點M,當P在圓周上運動時,點M的軌跡記為曲線C.
的圓,P為圓上一點,線段AP的垂直平分線l與直線PB交于點M,當P在圓周上運動時,點M的軌跡記為曲線C.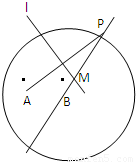
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com