
(本小題滿分14分)已知函數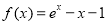 ,
, , 其中,
, 其中,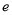 是自然對數的底數.函數
是自然對數的底數.函數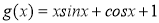 ,
, .
.
(Ⅰ)求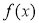 的最小值;
的最小值;
(Ⅱ)將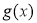 的全部零點按照從小到大的順序排成數列
的全部零點按照從小到大的順序排成數列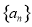 ,求證:
,求證:
(1)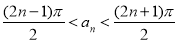 ,其中
,其中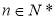 ;
;
(2)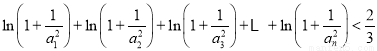 .
.
(Ⅰ)0(Ⅱ)證明見解析
【解析】
試題分析:(1)解決類似的問題時,注意區分函數的最值和極值.求函數的最值時,要先求函數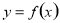 在區間
在區間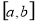 內使
內使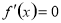 的點,再計算函數
的點,再計算函數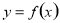 在區間內所有使
在區間內所有使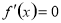 的點和區間端點處的函數值,最后比較即得;(2)證明不等式,利用函數的單調性很常見,一定要注意選取恰當的函數及單調區間(3)不等式具有放縮功能,常常用于證明不等式,解決問題的關鍵是分析不等式兩邊的結構特點,選擇好切入點.
的點和區間端點處的函數值,最后比較即得;(2)證明不等式,利用函數的單調性很常見,一定要注意選取恰當的函數及單調區間(3)不等式具有放縮功能,常常用于證明不等式,解決問題的關鍵是分析不等式兩邊的結構特點,選擇好切入點.
試題解析:(Ⅰ)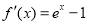 ,當
,當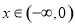 時,
時,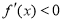 ;當
;當 時,
時,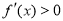 ;所以,函數
;所以,函數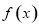 在
在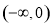 上是減函數,在
上是減函數,在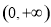 上是增函數,所以
上是增函數,所以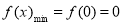 ,
,
綜上所述,函數 的最小值是0. 4分
的最小值是0. 4分
(Ⅱ)證明:對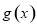 求導得
求導得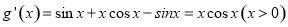 ,令
,令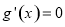 可得
可得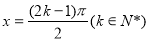 ,當
,當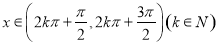 時,
時,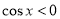 ,此時
,此時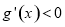 ;當
;當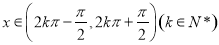 時,
時,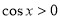 ,此時
,此時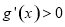 .所以,函數
.所以,函數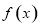 的單調遞減區間為
的單調遞減區間為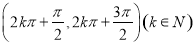 ,單調遞增區間為
,單調遞增區間為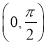 和
和 . 7分
. 7分
因為函數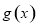 在區間
在區間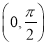 上單調遞增,又
上單調遞增,又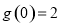 ,所以
,所以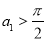 .當
.當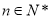 時,因為
時,因為 ,且函數
,且函數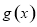 的圖像是連續不斷的,所以
的圖像是連續不斷的,所以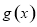 在區間
在區間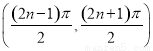 內至少存在一個零點,又
內至少存在一個零點,又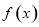 在區間
在區間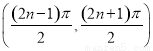 上是單調的,故
上是單調的,故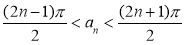 . 9分
. 9分
(2)證明:由(Ⅰ)知,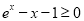 ,則
,則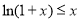 ,因此,當
,因此,當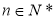 時,
時,
記S=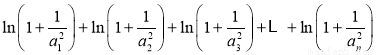
則S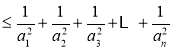 11分
11分
由(1)知,S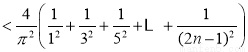
當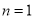 時,
時, ;
;
當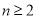 時,S
時,S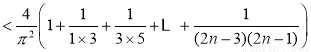
即,S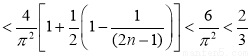 ,證畢. 14分
,證畢. 14分
考點:利用導數求函數最值,利用單調性及放縮法證明不等式.


科目:高中數學 來源:2014-2015學年山東省文登市高三上學期第一次考試理科數學試卷(解析版) 題型:選擇題
已知函數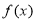 是奇函數,當
是奇函數,當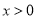 時,
時, ,且
,且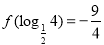 ,則
,則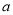 的值為( )
的值為( )
A.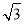 B.
B.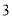 C.
C.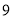 D.
D.
查看答案和解析>>
科目:高中數學 來源:2014-2015學年山東省濟寧市高三上學期期中考試文科數學試卷(解析版) 題型:選擇題
在正項等比數列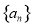 中,
中,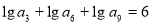 ,則
,則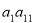 的值是 ( )
的值是 ( )
(A)10000 (B)1000 (C)100 (D)10
查看答案和解析>>
科目:高中數學 來源:2014-2015學年湖北省襄陽市高三上學期11月質檢文科數學試卷(解析版) 題型:填空題
傳說古希臘畢達哥拉斯學派的數學家經常在沙灘上面畫點或用小石子表示數.他們研究過如圖所示的三角形數:

將三角形數1,3,6,10,…記為數列{an},將可被5整除的三角形數按從小到大的順序組成一個新數列{bn},可以推測:(Ⅰ)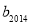 是數列
是數列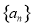 中的第_________項;(Ⅱ)若
中的第_________項;(Ⅱ)若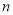 為正偶數,則
為正偶數,則 =_________.(用n表示)
=_________.(用n表示)
查看答案和解析>>
科目:高中數學 來源:2014-2015學年湖北省襄陽市高三上學期11月質檢文科數學試卷(解析版) 題型:選擇題
已知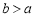 ,若函數
,若函數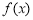 在定義域內的一個區間
在定義域內的一個區間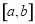 上函數值的取值范圍恰好是
上函數值的取值范圍恰好是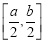 ,則稱區間
,則稱區間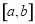 是函數
是函數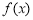 的一個減半壓縮區間,若函數
的一個減半壓縮區間,若函數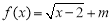 存在一個減半壓縮區間
存在一個減半壓縮區間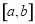 ,(
,(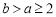 ),則實數m的取值范圍是( )
),則實數m的取值范圍是( )
A.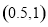 B.
B.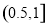 C.
C.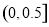 D.
D.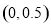
查看答案和解析>>
科目:高中數學 來源:2014-2015學年寧夏銀川市高一上學期9月月考數學試卷(解析版) 題型:解答題
(本小題滿分10分)已知集合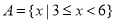 ,
,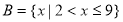 .
.
(Ⅰ)求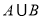 ,
,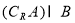 ;
;
(Ⅱ)已知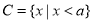 ,若
,若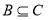 ,求實數
,求實數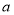 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com