
【題目】如圖,△ABC的外接圓⊙O的半徑為5,CE垂直于⊙O所在的平面,BD∥CE,CE=4,BC=6,且BD=1,![]() .
.
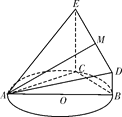
(1)求證:平面AEC⊥平面BCED;
(2)試問線段DE上是否存在點M,使得直線AM與平面ACE所成角的正弦值為![]() ?若存在,確定點M的位置;若不存在,請說明理由.
?若存在,確定點M的位置;若不存在,請說明理由.
【答案】(1)答案詳見解析;(2)存在,且![]() .
.
【解析】
試題(1)要證明面面垂直,只需證明一個平面另一個平面的一條垂線,本題在![]() 中,求得
中,求得![]() ,從而得
,從而得![]() 為⊙O的直徑,故
為⊙O的直徑,故![]() ,從而可證明
,從而可證明![]() 面
面![]() ,進而證明平面AEC⊥平面BCED;(2)以
,進而證明平面AEC⊥平面BCED;(2)以![]() 方向為
方向為![]() 軸的正方向建立空間直角坐標系,用坐標表示相關點,利用
軸的正方向建立空間直角坐標系,用坐標表示相關點,利用![]() 表示向量
表示向量![]() 的坐標,利用
的坐標,利用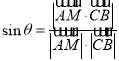 列方程求
列方程求![]() 的值,從而確定點
的值,從而確定點![]() 的位置.
的位置.
試題解析:(1)證明:∵![]() 平面
平面![]() .
.
∴![]() ,又因為
,又因為![]() ,
,![]() .
.
故AD=![]() ,AB=10=直徑長,(3分)
,AB=10=直徑長,(3分)
∴AC⊥BC.又因為EC⊥平面ABC,所以EC⊥BC.
∵AC∩EC=C,∴BC⊥平面ACE,又BC平面BCED,
∴平面AEC⊥平面BCED.(6分)
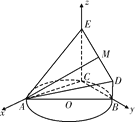
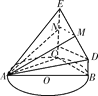
(2)法一:存在,如圖,以C為原點,直線CA為x軸,直線CB為y軸,直線CE為z軸建立空間直角坐標系,則有點的坐標,A(8,0,0),B(0,6,0),D(0,6,1),E(0,0,4).
則![]() =(-8,6,1),
=(-8,6,1),![]() =(0,-6,3),
=(0,-6,3),
設![]() =λ
=λ![]() =λ(0,-6,3)=(0,-6λ,3λ),0<λ<1
=λ(0,-6,3)=(0,-6λ,3λ),0<λ<1
故![]() =
=![]() +
+![]() =(-8, 6-6λ,1+3λ)
=(-8, 6-6λ,1+3λ)
由(1)易得平面ACE的法向量為![]() =(0,6,0),
=(0,6,0),
設直線AM與平面ACE所成角為θ,
則sin θ=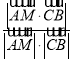 =
=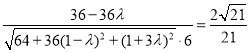 ,解得λ=
,解得λ=![]() .(10分)
.(10分)
所以存在點M,且![]() 時,直線AM與平面ACE所成角的正弦值為
時,直線AM與平面ACE所成角的正弦值為![]() . (12分)
. (12分)
法二:(幾何法)
如圖,作MN⊥CE交CE于N,連接AN,則MN⊥平面AEC,故直線AM與平面ACE所成的角為∠MAN,且MN⊥AN,NC⊥AC.
設MN=2x,由直線AM與平面ACE所成角的正弦值為![]() ,得AM=
,得AM=![]() x,所以AN=
x,所以AN=![]() x.
x.
另一方面,作DK∥MN∥BC,得EN=x,NC=4-x
而AC=8,故Rt△ANC中,由AN2=AC2+NC2
得17x2=64+(4-x)2,∴x=2,∴MN=4,EM=2![]()
所以存在點![]() ,且
,且![]() 時,直線
時,直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() . (12分)
. (12分)


科目:高中數學 來源: 題型:
【題目】給出下列說法:①方程![]() 表示的圖形是一個點;②命題“若
表示的圖形是一個點;②命題“若![]() ,則
,則![]() 或
或![]() ”為真命題;③已知雙曲線
”為真命題;③已知雙曲線![]() 的左右焦點分別為
的左右焦點分別為![]() ,
,![]() ,過右焦點
,過右焦點![]() 被雙曲線截得的弦長為4的直線有3條;④已知橢圓
被雙曲線截得的弦長為4的直線有3條;④已知橢圓![]() 上有兩點
上有兩點![]() ,
,![]() ,若點
,若點![]() 是橢圓
是橢圓![]() 上任意一點,且
上任意一點,且![]() ,直線
,直線![]() ,
,![]() 的斜率分別為
的斜率分別為![]() ,
,![]() ,則
,則![]() 為定值
為定值![]() .
.
其中說法正確的序號是________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() ,過點
,過點![]() 的直線與拋物線
的直線與拋物線![]() 相切,設第一象限的切點為
相切,設第一象限的切點為![]() .
.
(1)求點![]() 的坐標;
的坐標;
(2)若過點![]() 的直線
的直線![]() 與拋物線
與拋物線![]() 相交于兩點
相交于兩點![]() ,圓
,圓![]() 是以線段
是以線段![]() 為直徑的圓過點
為直徑的圓過點![]() ,求直線
,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國有一道古典數學名著——兩鼠穿墻:“今有垣厚十尺,兩鼠對穿,初日各一尺,大鼠日自倍,小鼠日自半,問幾何日相逢?”題意是:“有兩只老鼠從墻的兩邊打洞穿墻(連線與墻面垂直),大老鼠第一天進一尺,以后每天加倍,小老鼠第一天也進一尺,以后每天減半,那么兩鼠第幾天能見面.”假設墻厚16尺,如圖是源于該題思想的一個程序框圖,則輸出的![]() ( )
( )

A. 3 B. 4 C. 5 D. 6
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】盡管目前人類還無法準確預報地震,但科學家通過研究,已經對地震有所了解,例如,地震釋放出的能量![]() (單位:焦耳)與地震里氏震級
(單位:焦耳)與地震里氏震級![]() 之間的關系為
之間的關系為![]() .
.
(1)已知地震等級劃分為里氏![]() 級,根據等級范圍又分為三種類型,其中小于
級,根據等級范圍又分為三種類型,其中小于![]() 級的為“小地震”,介于
級的為“小地震”,介于![]() 級到
級到![]() 級之間的為“有感地震”,大于
級之間的為“有感地震”,大于![]() 級的為“破壞性地震”若某次地震釋放能量約
級的為“破壞性地震”若某次地震釋放能量約![]() 焦耳,試確定該次地震的類型;
焦耳,試確定該次地震的類型;
(2)2008年汶川地震為里氏![]() 級,2011年日本地震為里氏
級,2011年日本地震為里氏![]() 級,問:2011年日本地震所釋放的能量是2008年汶川地震所釋放的能量的多少倍? (取
級,問:2011年日本地震所釋放的能量是2008年汶川地震所釋放的能量的多少倍? (取![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某小電子產品2018年的價格為9元/件,年銷量為![]() 件,經銷商計劃在2019年將該電子產品的價格降為
件,經銷商計劃在2019年將該電子產品的價格降為![]() 元/件(其中
元/件(其中![]() ),經調查,顧客的期望價格為5元/件,經測算,該電子產品的價格下降后年銷量新增加了
),經調查,顧客的期望價格為5元/件,經測算,該電子產品的價格下降后年銷量新增加了![]() 件(其中常數
件(其中常數![]() ).已知該電子產品的成本價格為4元/件.
).已知該電子產品的成本價格為4元/件.
(1)寫出該電子產品價格下降后,經銷商的年收益![]() 與實際價格
與實際價格![]() 的函數關系式:(年收益=年銷售收入-成本)
的函數關系式:(年收益=年銷售收入-成本)
(2)設![]() ,當實際價格最低定為多少時,仍然可以保證經銷商2019年的收益比2018年至少增長20%?
,當實際價格最低定為多少時,仍然可以保證經銷商2019年的收益比2018年至少增長20%?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某輛汽車以![]() 千米
千米![]() 小時的速度在高速公路上勻速行駛(考慮到高速公路行車安全要求
小時的速度在高速公路上勻速行駛(考慮到高速公路行車安全要求![]() 時,每小時的油耗(所需要的汽油量)為
時,每小時的油耗(所需要的汽油量)為![]() 升,其中
升,其中![]() 為常數,且
為常數,且![]() .
.
(1)若汽車以120千米![]() 小時的速度行駛時,每小時的油耗為11.5升,欲使每小時的油耗不超過9升,求
小時的速度行駛時,每小時的油耗為11.5升,欲使每小時的油耗不超過9升,求![]() 的取值范圍;
的取值范圍;
(2)求該汽車行駛100千米的油耗的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com