【題目】設 
，向量 
=（cosα，sinα）， 
．
（1）證明：向量 
與 
垂直；
（2）當| 
|=| 
|時，求角α．
【答案】
（1）證明：由向量 
=（cosα，sinα）， 
，
得| |=1， 
=1，則 
，
所以向量 
與 
垂直
（2）解：將| 
|=| 
|兩邊平方，化簡得3（| |2﹣| 
|2）+8 
，
由| |= =1，得 ，即 
．
所以 
，注意到 
，得 
【解析】（1）計算| |， ，通過計算 ，證明向量 與 垂直；（2）將| |=| |兩邊平方，平方可得3（| |2﹣| |2）+8 ，從而得到以 ，然后求角α．
【考點精析】解答此題的關鍵在于理解數量積表示兩個向量的夾角的相關知識，掌握設
、
都是非零向量，
，
，
是與
的夾角，則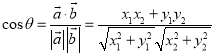
，以及對數量積判斷兩個平面向量的垂直關系的理解，了解若平面
的法向量為
，平面
的法向量為
，要證
，只需證
，即證
;即：兩平面垂直
兩平面的法向量垂直．
名校課堂系列答案科目：高中數學 來源： 題型：
【題目】已知甲、乙兩個容器，甲容器容量為
，裝滿純酒精，乙容器容量為
，其中裝有體積為
的水（
：單位： 
）.現將甲容器中的液體倒人乙容器中，直至甲容器中液體倒完或乙容器盛滿，攪拌使乙容器中兩種液體充分混合，再將乙容器中的液體倒人甲容器中直至倒滿，攪拌使甲容器中液體充分混合，如此稱為一次操作，假設操作過程中溶液體積變化忽略不計.設經過
次操作之后，乙容器中含有純酒精
（單位： 
），下列關于數列
的說法正確的是（ ）
A. 當
時，數列
有最大值
B. 設
，則數列
為遞減數列
C. 對任意的
，始終有
D. 對任意的
，都有
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
： 
（
）與
軸交于
， 
兩點， 
為橢圓
的左焦點，且
是邊長為2的等邊三角形.
（Ⅰ）求橢圓
的方程；
（Ⅱ）設直線
與橢圓
交于
， 
兩點，點
關于
軸的對稱點為
（
與
不重合），則直線
與
軸交于點
，求
面積的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】濰坊文化藝術中心的觀光塔是濰坊市的標志性建筑，某班同學準備測量觀光塔
的高度
（單位：米），如圖所示，垂直放置的標桿
的高度
米，已知
， 
.
（1）該班同學測得
一組數據： 
，請據此算出
的值；
（2）該班同學分析若干測得的數據后，發現適當調整標桿到觀光塔的距離
（單位：米），使
與
的差較大，可以提高測量精確度，若觀光塔高度為136米，問
為多大時， 
的值最大？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知左、右焦點分別為
的橢圓
與直線
相交于
兩點，使得四邊形
為面積等于
的矩形.
（1）求橢圓
的方程；
（2）過橢圓
上一動點
（不在
軸上）作圓
的兩條切線
，切點分別為
，直線
與橢圓
交于
兩點， 
為坐標原點，求
的面積
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知
為坐標原點，設動點
.
（1）當
時，若過點
的直線
與圓
：
相切，求直線的方程；
（2）當
時，求以
為直徑且被直線
截得的弦長為2的圓的方程；
（3）當時，設
，過點
作的垂線，與以為直徑的圓交于點
，垂足為
，試問：線段
的長是否為定值？若為定值，求出這個定值；若不為定值，請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
