【題目】選修4-5：不等式選講
設函數
．
（1）證明：
；
（2）若不等式
的解集是非空集，求
的范圍．
【答案】（1）見解析；（2）
.
【解析】試題分析：（1）直接計算
，由絕對值不等式的性質及基本不等式證之即可；
（2）
，分區間討論去絕對值符號分別解不等式即可.
試題解析： （1）證明：函數f（x）=|x﹣a|，a＜0，
則f（x）+f（﹣
）=|x﹣a|+|﹣﹣a|=|x﹣a|+|
+a|≥|（x﹣a）+（+a）|
=|x+|=|x|+
≥2
=2．
（2）f（x）+f（2x）=|x﹣a|+|2x﹣a|，a＜0．
當x≤a時，f（x）=a﹣x+a﹣2x=2a﹣3x，則f（x）≥﹣a；
當a＜x＜
時，f（x）=x﹣a+a﹣2x=﹣x，則﹣＜f（x）＜﹣a；
當x
時，f（x）=x﹣a+2x﹣a=3x﹣2a，則f（x）≥﹣．則f（x）的值域為[﹣
，+∞）.
不等式f（x）+f（2x）＜
的解集非空，即為＞﹣，解得，a＞﹣1，由于a＜0，
則a的取值范圍是．
科目：高中數學 來源： 題型：
【題目】橢圓
的中心在坐標原點，焦點在
軸上，焦點到短軸端點的距離為2，離心率為
.
（Ⅰ）求該橢圓的方程；
（Ⅱ）若直線
與橢圓
交于
， 
兩點且
，是否存在以原點
為圓心的定圓與直線
相切？若存在求出定圓的方程；若不存在，請說明理由
查看答案和解析>>
科目：高中數學 來源： 題型：
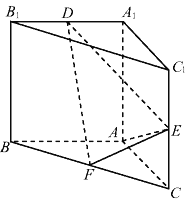
【題目】直三棱柱
中, 
分別是
的中點, 且
,
(1)證明: 
.
(2)棱
上是否存在一點
,使得平面
與平面
所成銳二面角的余弦值為
若存在,說明點
的位置,若不存在,說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
(1)若函數
的圖象與x軸無交點，求a的取值范圍；
(2) 若函數
在[-1,1]上存在零點，求a的取值范圍；
(3)設函數
，當
時，若對任意的
，總存在
，使得
，求b的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】甲乙兩人參加某種選拔測試，在備選的10道題中，甲答對其中每道題的概率都是
，乙能答對其中的8道題．規定每次考試都從備選的10道題中隨機抽出4道題進行測試，只有選中的4個題目均答對才能入選；
（Ⅰ）求甲恰有2個題目答對的概率及甲答對題目數
的數學期望與方差。
（Ⅱ）求乙答對的題目數X的分布列。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知命題P:函數
是增函數，命題Q:
（1）寫出命題Q的否命題
，并求出實數
的取值范圍，使得命題為真命題；
（2）如果
是真命題，
是假命題，求實數的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
