
分析 (Ⅰ)由x=ρcosθ,y=ρsinθ,能求出曲線C1的直角坐標方程.
(Ⅱ)設Q(cosθ,sinθ),(θ∈[-$\frac{π}{2}$,$\frac{π}{2}$]),由題意知直線C的斜率k=$\sqrt{3}$,從而$\frac{sinθ}{cosθ}$=tanθ=-$\frac{\sqrt{3}}{3}$,進而Q($\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$).設A,B對應的參數分別為t1,t2.把$\left\{\begin{array}{l}{x=\frac{\sqrt{3}}{2}+\frac{1}{2}t}\\{y=-\frac{1}{2}+\frac{\sqrt{3}}{2}t}\end{array}\right.$,代入y2=4x,得3t2-(8+2$\sqrt{3}$)t-8$\sqrt{3}+1$=0,由此利用韋達定理能求出|AQ|-|BQ|.
解答 解:(Ⅰ)∵x=ρcosθ,y=ρsinθ,
由ρsin2θ=4cosθ,得ρ2sin2θ=4ρcosθ,
∴曲線C1的直角坐標方程為:y2=4x.
(Ⅱ)設Q(cosθ,sinθ),(θ∈[-$\frac{π}{2}$,$\frac{π}{2}$]),由題意知直線C的斜率k=$\sqrt{3}$,
所以${k}_{OQ}=-\frac{\sqrt{3}}{3}$,即$\frac{sinθ}{cosθ}$=tanθ=-$\frac{\sqrt{3}}{3}$,
所以$θ=-\frac{π}{6}$,故Q($\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$).
取${x}_{0}=\frac{\sqrt{3}}{2}$,${y}_{0}=-\frac{1}{2}$,不妨設A,B對應的參數分別為t1,t2.
把$\left\{\begin{array}{l}{x=\frac{\sqrt{3}}{2}+\frac{1}{2}t}\\{y=-\frac{1}{2}+\frac{\sqrt{3}}{2}t}\end{array}\right.$,代入y2=4x,
化簡得$\frac{3{t}^{2}}{4}=4(2+\frac{t}{2})$,即3t2-(8+2$\sqrt{3}$)t-8$\sqrt{3}+1$=0,
∵C與C1相交于A,B,∴△>0,t1+t2=$\frac{8+2\sqrt{3}}{3}$.
∴|AQ|-|BQ|=|t1+t2|=$\frac{8+2\sqrt{3}}{3}$.
點評 本題考查曲線的直角坐標的求法,考查兩線段之差的求法,考查極坐標方程、直角坐標方程、參數方程的互化等基礎知識,考查推理論證能力、運算求解能力,考查化歸與轉化思想、函數與方程思想,是中檔題.


 金鑰匙試卷系列答案
金鑰匙試卷系列答案科目:高中數學 來源: 題型:選擇題
| A. | $\frac{100π}{3}$ | B. | 64π | C. | 100π | D. | $\frac{500π}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\sqrt{7}$ | B. | 3 | C. | $\sqrt{11}$ | D. | $\sqrt{13}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
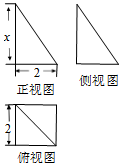
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | 2 | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com