
【題目】各項均為正數(shù)的數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,且滿足
,且滿足![]() ,
,![]() ,
,![]() .各項均為正數(shù)的等比數(shù)列
.各項均為正數(shù)的等比數(shù)列![]() 滿足
滿足![]() ,
,![]() .
.
(1)求數(shù)列![]() 、
、![]() 的通項公式;
的通項公式;
(2)若![]() ,數(shù)列
,數(shù)列![]() 的前
的前![]() 項和
項和![]() .
.
①求![]() ;
;
②若對任意![]() ,
,![]() ,均有
,均有![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ,
,![]() ;(2)①
;(2)①![]() ;②
;②![]() .
.
【解析】
(1)令![]() 可求得
可求得![]() ,再令
,再令![]() ,由
,由![]() 得
得![]() ,兩式作差并結合已知條件得出
,兩式作差并結合已知條件得出![]() ,結合
,結合![]() 可知數(shù)列
可知數(shù)列![]() 是等差數(shù)列,確定數(shù)列
是等差數(shù)列,確定數(shù)列![]() 的首項和公差,可求得
的首項和公差,可求得![]() ,并根據(jù)已知條件求出等比數(shù)列
,并根據(jù)已知條件求出等比數(shù)列![]() 的首項和公比,由此可求得
的首項和公比,由此可求得![]() ;
;
(2)①求得![]() ,利用錯位相減法可求得
,利用錯位相減法可求得![]() ;
;
②由題意可得![]() 對任意的
對任意的![]() 且
且![]() 恒成立,由參變量分離法得
恒成立,由參變量分離法得![]() ,構造數(shù)列
,構造數(shù)列![]() ,利用定義判斷數(shù)列
,利用定義判斷數(shù)列![]() 的單調性,求得數(shù)列
的單調性,求得數(shù)列![]() 的最大項,由此可得出實數(shù)
的最大項,由此可得出實數(shù)![]() 的取值范圍.
的取值范圍.
(1)對任意的![]() ,
,![]() .
.
當![]() 時,
時,![]() ,即
,即![]() ,解得
,解得![]() ;
;
當![]() 時,由
時,由![]() 得
得![]() ,
,
兩式作差得![]() ,即
,即![]() ,
,
又因為數(shù)列![]() 各項均為正數(shù),則
各項均為正數(shù),則![]() ,所以,
,所以,![]() ,
,
又![]() ,所以,數(shù)列
,所以,數(shù)列![]() 是等差數(shù)列,且首項為
是等差數(shù)列,且首項為![]() ,公差為
,公差為![]() ,
,
![]() .
.
設等比數(shù)列![]() 的公比為
的公比為![]() ,則
,則![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() ;
;
(2)①![]() ,
,![]() ,
,
![]() ,
,
上述兩式作差得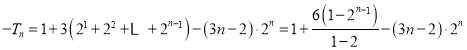
![]() ,
,
因此,![]() ;
;
②由題意可知![]() 對任意的
對任意的![]() 且
且![]() 恒成立,
恒成立,
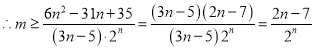 ,即
,即![]() 恒成立,
恒成立,
設![]() ,
,![]() ,
,
當![]() 時,
時,![]() ,此時數(shù)列
,此時數(shù)列![]() 單調遞增,即
單調遞增,即![]() ;
;
當![]() 時,
時,![]() ,此時數(shù)列
,此時數(shù)列![]() 單調遞減,即
單調遞減,即![]() .
.
所以,數(shù)列![]() 中最大項為
中最大項為![]() ,
,![]() .
.
因此,實數(shù)![]() 的取值范圍是
的取值范圍是![]() .
.


 能力評價系列答案
能力評價系列答案 唐印文化課時測評系列答案
唐印文化課時測評系列答案科目:高中數(shù)學 來源: 題型:
【題目】現(xiàn)從某醫(yī)院中隨機抽取了七位醫(yī)護人員的關愛患者考核分數(shù)(患者考核: ![]() 分制),用相關的特征量
分制),用相關的特征量![]() 表示;醫(yī)護專業(yè)知識考核分數(shù)(試卷考試:
表示;醫(yī)護專業(yè)知識考核分數(shù)(試卷考試: ![]() 分制),用相關的特征量
分制),用相關的特征量![]() 表示,數(shù)據(jù)如下表:
表示,數(shù)據(jù)如下表:
特征量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 98 | 88 | 96 | 91 | 90 | 92 | 96 |
| 9.9 | 8.6 | 9.5 | 9.0 | 9.1 | 9.2 | 9.8 |
(1)求![]() 關于
關于![]() 的線性回歸方程(計算結果精確到
的線性回歸方程(計算結果精確到![]() );
);
(2)利用(1)中的線性回歸方程,分析醫(yī)護專業(yè)考核分數(shù)的變化對關愛患者考核分數(shù)的影響,并估計某醫(yī)護人員的醫(yī)護專業(yè)知識考核分數(shù)為![]() 分時,他的關愛患者考核分數(shù)(精確到
分時,他的關愛患者考核分數(shù)(精確到![]() );
);
(3)現(xiàn)要從醫(yī)護專業(yè)知識考核分數(shù)![]() 分以下的醫(yī)護人員中選派
分以下的醫(yī)護人員中選派![]() 人參加組建的“九寨溝災后醫(yī)護小分隊”培訓,求這兩人中至少有一人考核分數(shù)在
人參加組建的“九寨溝災后醫(yī)護小分隊”培訓,求這兩人中至少有一人考核分數(shù)在![]() 分以下的概率.
分以下的概率.
附:回歸方程![]() 中斜率和截距的最小二乘法估計公式分別為
中斜率和截距的最小二乘法估計公式分別為 ,
, ![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某生物研究者于元旦在湖中放入一些鳳眼蓮,這些鳳眼蓮在湖中的蔓延速度越來越快,二月底測得鳳眼蓮覆蓋面積為![]() ,三月底測得鳳眼蓮覆蓋面積為
,三月底測得鳳眼蓮覆蓋面積為![]() ,鳳眼蓮覆蓋面積
,鳳眼蓮覆蓋面積![]() (單位:
(單位:![]() )與月份
)與月份![]() (單位:月)的關系有兩個函數(shù)模型
(單位:月)的關系有兩個函數(shù)模型![]() 與
與![]() 可供選擇.
可供選擇.
(1)試判斷哪個函數(shù)模型更合適并求出該模型的解析式;
(2)求鳳眼蓮覆蓋面積是元旦放入面積![]() 倍以上的最小月份.
倍以上的最小月份.
(參考數(shù)據(jù)![]() ,
,![]() )
)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某學校為鼓勵家校互動,與某手機通訊商合作,為教師辦理流量套餐.為了解該校教師手機流量使用情況,通過抽樣,得到![]() 位教師近
位教師近![]() 年每人手機月平均使用流量
年每人手機月平均使用流量![]() (單位:
(單位:![]() )的數(shù)據(jù),其頻率分布直方圖如下:
)的數(shù)據(jù),其頻率分布直方圖如下:

若將每位教師的手機月平均使用流量分別視為其手機月使用流量,并將頻率為概率,回答以下問題.
(Ⅰ) 從該校教師中隨機抽取![]() 人,求這
人,求這![]() 人中至多有
人中至多有![]() 人月使用流量不超過
人月使用流量不超過![]()
![]() 的概率;
的概率;
(Ⅱ) 現(xiàn)該通訊商推出三款流量套餐,詳情如下:
套餐名稱 | 月套餐費(單位:元) | 月套餐流量(單位: |
|
|
|
|
|
|
|
|
|
這三款套餐都有如下附加條款:套餐費月初一次性收取,手機使用一旦超出套餐流量,系統(tǒng)就自動幫用戶充值![]()
![]() 流量,資費
流量,資費![]() 元;如果又超出充值流量,系統(tǒng)就再次自動幫用戶充值
元;如果又超出充值流量,系統(tǒng)就再次自動幫用戶充值![]()
![]() 流量,資費
流量,資費![]() 元/次,依次類推,如果當月流量有剩余,系統(tǒng)將自動清零,無法轉入次月使用.
元/次,依次類推,如果當月流量有剩余,系統(tǒng)將自動清零,無法轉入次月使用.
學校欲訂購其中一款流量套餐,為教師支付月套餐費,并承擔系統(tǒng)自動充值的流量資費的![]() ,其余部分由教師個人承擔,問學校訂購哪一款套餐最經(jīng)濟?說明理由.
,其余部分由教師個人承擔,問學校訂購哪一款套餐最經(jīng)濟?說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在古代,直角三角形中較短的直角邊稱為“勾”,較長的直角邊稱為“股”,斜邊稱為“弦”.三國時期吳國數(shù)學家趙爽用“弦圖”( 如圖) 證明了勾股定理,證明方法敘述為:“按弦圖,又可以勾股相乘為朱實二,倍之為朱實四,以勾股之差自相乘為中黃實,加差實,亦成弦實.”這里的“實”可以理解為面積.這個證明過程體現(xiàn)的是這樣一個等量關系:“兩條直角邊的乘積是兩個全等直角三角形的面積的和(朱實二 ),4個全等的直角三角形的面積的和(朱實四) 加上中間小正方形的面積(黃實) 等于大正方形的面積(弦實)”. 若弦圖中“弦實”為16,“朱實一”為![]() ,現(xiàn)隨機向弦圖內投入一粒黃豆(大小忽略不計),則其落入小正方形內的概率為( )
,現(xiàn)隨機向弦圖內投入一粒黃豆(大小忽略不計),則其落入小正方形內的概率為( )
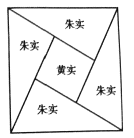
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】現(xiàn)有4種不同顏色要對如圖所示的四個部分進行著色,要求有公共邊界的兩部分不能用同一種顏色,則不同的著色方法共有( )

A. 144種 B. 72種 C. 64種 D. 84種
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() (
(![]() ).
).
(1)當![]() 時,求函數(shù)
時,求函數(shù)![]() 的單調區(qū)間;
的單調區(qū)間;
(2)若函數(shù)![]() 的圖象在點
的圖象在點![]() 處的切線的傾斜角為
處的切線的傾斜角為![]() ,且函數(shù)
,且函數(shù)![]() (
(![]() )當且僅當在
)當且僅當在![]() 處取得極值,其中
處取得極值,其中![]() 為
為![]() 的導函數(shù),求
的導函數(shù),求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】拋物線頂點在原點,焦點在x軸上,且過點(4,4),焦點為F.
(1)求拋物線的焦點坐標和標準方程;
(2)P是拋物線上一動點,M是PF的中點,求M的軌跡方程.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】為比較甲、乙兩地某月14時的氣溫狀況,隨機選取該月中的5天,將這5天中14時的氣溫數(shù)據(jù)(單位:℃)制成如圖所示的莖葉圖.考慮以下結論:
①甲地該月14時的平均氣溫低于乙地該月14時的平均氣溫;
②甲地該月14時的平均氣溫高于乙地該月14時的平均氣溫;
③甲地該月14時的平均氣溫的標準差小于乙地該月14時的氣溫的標準差;
④甲地該月14時的平均氣溫的標準差大于乙地該月14時的氣溫的標準差.
其中根據(jù)莖葉圖能得到的統(tǒng)計結論的標號為( )
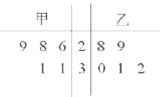
A.①③B.①④C.②③D.②④
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com