【題目】已知點M（2，0），圓C：x2+y2+4x=0.
（1）求直線3x+4y+1=0與圓C：x2+y2+4x=0相交所得的弦長|MN|；
（2）過點M的直線與圓C交于A，B兩個不同的點，求弦AB的中點P的軌跡方程.
【答案】（1）2
；（2）x2+y2=4，（x<﹣1）.
【解析】
（1）將圓的方程轉化為標準形式，求出圓心與半徑，再利用點到直線的距離公式求出圓心到直線的距離，從而可求出弦長|MN|=2
2
.
（2）當M與P不重合時，連結CP，則CP⊥MP，從而可得|CP|2+|MP|2=|CM|2，設P（x，y），利用兩點間的距離公式列方程即可求解.
（1）圓C：x2+y2+4x=0
可得圓C：（x+2）2+y2=4，圓心坐標（﹣2，0）半徑為2，
圓的圓心到直線的距離為：d
1，
∴直線3x+4y+1=0與圓C：x2+y2+4x=0相交所得的弦長|MN|=22；
（2）解：當M與P不重合時，連結CP，則CP⊥MP，
∴|CP|2+|MP|2=|CM|2，
設P（x，y），則（x+2）2+y2+（x﹣2）2+y2=16，
化簡得：x2+y2=4（x<﹣1），
故弦AB中點P的軌跡方程是x2+y2=4，（x<﹣1）.
53隨堂測系列答案科目：高中數學 來源： 題型：
【題目】如圖，某旅游區擬建一主題游樂園，該游樂區為五邊形區域ABCDE，其中三角形區域ABE為主題游樂區，四邊形區域為BCDE為休閑游樂區，AB、BC，CD，DE，EA，BE為游樂園的主要道路（不考慮寬度）．
.
（I）求道路BE的長度；
（Ⅱ）求道路AB，AE長度之和的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】鳳鳴山中學的高中女生體重
(單位：kg)與身高
(單位：cm)具有線性相關關系，根據一組樣本數據
（
），用最小二乘法近似得到回歸直線方程為
，則下列結論中不正確的是（ ）
A.與具有正線性相關關系
B.回歸直線過樣本的中心點
C.若該中學某高中女生身高增加1cm，則其體重約增加0.85kg
D.若該中學某高中女生身高為160cm，則可斷定其體重必為50.29kg.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某機構組織語文、數學學科能力競賽，按照一定比例淘汰后，頒發一二三等獎.現有某考場的兩科考試成績數據統計如下圖所示，其中數學科目成績為二等獎的考生有
人.
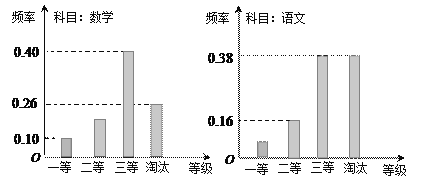
（Ⅰ）求該考場考生中語文成績為一等獎的人數；
（Ⅱ）用隨機抽樣的方法從獲得數學和語文二等獎的學生中各抽取
人，進行綜合素質測試，將他們的綜合得分繪成莖葉圖，求樣本的平均數及方差并進行比較分析；
（Ⅲ）已知本考場的所有考生中，恰有
人兩科成績均為一等獎，在至少一科成績為一等獎的考生中，隨機抽取
人進行訪談，求兩人兩科成績均為一等獎的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
