
【題目】如圖1,在正方形![]() 中,點
中,點![]() 分別是
分別是![]() 的中點,
的中點,![]() 與
與![]() 交于點
交于點![]() ,點
,點![]() 分別在線段
分別在線段![]() 上,且
上,且![]() .將
.將![]() 分別沿
分別沿![]() 折起,使點
折起,使點![]() 重合于點
重合于點![]() ,如圖2所示.
,如圖2所示.
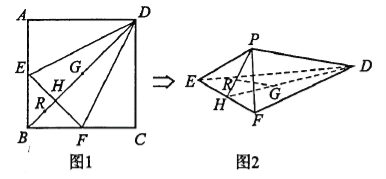
(1)求證:![]() 平面
平面![]() ;
;
(2)若正方形![]() 的邊長為4,求三棱錐
的邊長為4,求三棱錐![]() 的內切球的半徑.
的內切球的半徑.
【答案】(1)詳見解析;(2)![]() .
.
【解析】
試題分析:(1)因為點![]() 重合于點
重合于點![]() (該點記為
(該點記為![]() ),由原圖可知,
),由原圖可知,![]() 三條直線兩兩垂直,那么
三條直線兩兩垂直,那么![]() 平面
平面![]() ,又根據圖中給的比例關系,可知
,又根據圖中給的比例關系,可知![]() ,根據平行關系可知
,根據平行關系可知![]() ,平行線與同一平面垂直,即證明;(2)因為內切球的球心到三棱錐的四個面的距離相等,所以可將三棱錐的體積分為四個小三棱錐的體積和,而每一個小三棱錐的高就是內切球的半徑
,平行線與同一平面垂直,即證明;(2)因為內切球的球心到三棱錐的四個面的距離相等,所以可將三棱錐的體積分為四個小三棱錐的體積和,而每一個小三棱錐的高就是內切球的半徑![]() ,這樣根據體積和可求得內切球的半徑.
,這樣根據體積和可求得內切球的半徑.
試題解析:(1)在正方形![]() 中,
中,![]() 為直角,
為直角,
∴在三棱錐![]() 中,
中,![]() 三條線段兩兩垂直...................2分
三條線段兩兩垂直...................2分
∴![]() 平面
平面![]() ...........................3分
...........................3分
∵![]() ,即
,即![]() ,∴在
,∴在![]() 中,
中,![]() ...............4分
...............4分
∴![]() 平面
平面![]() ....................6分
....................6分
(2)正方形![]() 邊長為4.
邊長為4.
由題意,![]() ...................7分
...................7分
∴![]() .
.
![]() ..................10分
..................10分
設三棱錐![]() 內切球半徑為
內切球半徑為![]() .
.
則三棱錐的體積![]()
∴![]() .
.
∴三棱錐![]() 的內切球的半徑為
的內切球的半徑為![]() .....................12分
.....................12分


 培優三好生系列答案
培優三好生系列答案 優化作業上海科技文獻出版社系列答案
優化作業上海科技文獻出版社系列答案科目:高中數學 來源: 題型:
【題目】已知雙曲線![]() 的離心率為
的離心率為![]() ,圓心在
,圓心在![]() 軸的正半軸上的圓
軸的正半軸上的圓![]() 與雙曲線的漸近線相切,且圓
與雙曲線的漸近線相切,且圓![]() 的半徑為2,則以圓
的半徑為2,則以圓![]() 的圓心為焦點的拋物線的標準方程為( )
的圓心為焦點的拋物線的標準方程為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知x=1是函數f(x)=![]() ax3-
ax3-![]() x2+(a+1)x+5的一個極值點.
x2+(a+1)x+5的一個極值點.
(1)求函數f(x)的解析式;
(2)若曲線y=f(x)與直線y=2x+m有三個交點,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
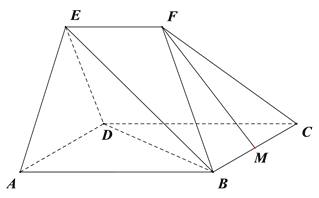
【題目】如圖,在幾何體![]() 中,平面
中,平面![]() 平面
平面![]() ,四邊形
,四邊形![]() 為菱形,且
為菱形,且![]() ,
, ![]() ,
, ![]() ∥
∥![]() ,
, ![]() 為
為![]() 中點.
中點.
(Ⅰ)求證: ![]() ∥平面
∥平面![]() ;
;
(Ⅱ)求直線![]() 與平面
與平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)在棱![]() 上是否存在點
上是否存在點![]() ,使
,使![]()
![]() ? 若存在,求
? 若存在,求![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知過原點的動直線l與圓![]() 相交于不同的兩點A,B.
相交于不同的兩點A,B.
(1)求線段AB的中點M的軌跡C的方程;
(2)是否存在實數k,使得直線L:y=k(x﹣4)與曲線C只有一個交點?若存在,求出k的取值范圍;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com