
| A. | ac<bc | B. | abc<bac | C. | ca<cb | D. | logac<logbc |
分析 根據冪函數的單調性和條件判斷A和B,根據指數函數的單調性判斷C,根據對數函數的單調性和對數的運算性質判斷D.
解答 解:A、因為0<c<1,所以函數y=xc在(0,+∞)上遞增,
又a>b>1,則ac>bc,A不正確;
B、因為0<c<1,所以c-1<0,函數y=xc-1在(0,+∞)上遞減,
又a>b>1,則ac-1<bc-1,兩邊同除以ab可得:abc>bac,B不正確;
C、因為0<c<1,所以函數y=cx在定義域上遞減,
又a>b>1,則cb>ca,C正確;
D、因為0<c<1,所以函數$y=lo{g}_{c}^{x}$在(0,+∞)上遞減,
又a>b>1,則$lo{g}_{c}^{a}<lo{g}_{c}^{b}<0$,即$\frac{1}{lo{g}_{c}^{a}}>\frac{1}{lo{g}_{c}^{b}}$,
所以$lo{g}_{a}^{c}>lo{g}_{b}^{c}$,D不正確,
故選:C.
點評 本題考查了冪函數、指數函數、對數函數的單調性,以及對數運算性質的應用,屬于基礎題.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 5 | B. | $\sqrt{5}$ | C. | $\sqrt{17}$ | D. | $\sqrt{17}$或$\frac{\sqrt{17}}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
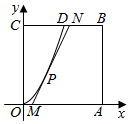 某地要建造一個邊長為2(單位:km)的正方形市民休閑公園OABC,將其中的區域ODC開挖成一個池塘,如圖建立平面直角坐標系后,點D的坐標為(1,2),曲線OD是函數y=ax2圖象的一部分,對邊OA上一點M在區域OABD內作一次函數y=kx+b(k>0)的圖象,與線段DB交于點N(點N不與點D重合),且線段MN與曲線OD有且只有一個公共點P,四邊形MABN為綠化風景區:
某地要建造一個邊長為2(單位:km)的正方形市民休閑公園OABC,將其中的區域ODC開挖成一個池塘,如圖建立平面直角坐標系后,點D的坐標為(1,2),曲線OD是函數y=ax2圖象的一部分,對邊OA上一點M在區域OABD內作一次函數y=kx+b(k>0)的圖象,與線段DB交于點N(點N不與點D重合),且線段MN與曲線OD有且只有一個公共點P,四邊形MABN為綠化風景區:查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com