
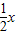 )n展開式的各項依次記為a1(x),a2(x),a3(x)…an(x),an+1(x).設F(x)=a1(x)+2a2(x)+2a2(x)+3a3(x)…+nan(x)+(n+1)an+1(x).
)n展開式的各項依次記為a1(x),a2(x),a3(x)…an(x),an+1(x).設F(x)=a1(x)+2a2(x)+2a2(x)+3a3(x)…+nan(x)+(n+1)an+1(x).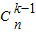 •
•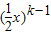 ,求得a1(x),a2(x),a3(x)的系數,根據前三項的系數成等差數列求得n的值.
,求得a1(x),a2(x),a3(x)的系數,根據前三項的系數成等差數列求得n的值.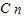 +2
+2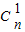 +3
+3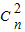 +…+(n+1)
+…+(n+1)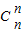 ,設Sn=
,設Sn=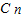 +2
+2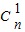 +3
+3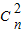 +…+(n+1)
+…+(n+1)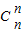 ,利用二項式系數的性質求得Sn=(n+2)•2n-2.再利用導數可得F(x)在[0,2]上是增函數可得對任意x1,x2∈[0,2],恒有|F(x1)-F(x2)|≤F(2)-F(0)=2n-1(n+2)-1.
,利用二項式系數的性質求得Sn=(n+2)•2n-2.再利用導數可得F(x)在[0,2]上是增函數可得對任意x1,x2∈[0,2],恒有|F(x1)-F(x2)|≤F(2)-F(0)=2n-1(n+2)-1.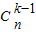 •
•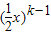 ,k=1、2、3,…n+1,
,k=1、2、3,…n+1,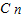 =1,
=1,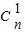 •
• =
=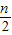 ,
,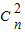
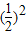 =
=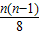 .
.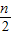 =1+
=1+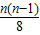 ,解得 n=8.
,解得 n=8.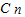 +2
+2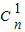 •(
•(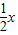 )+3
)+3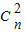 •
•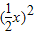 +(n+1)
+(n+1)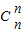 •
•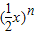 ,
,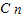 +2
+2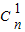 +3
+3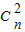 +…+(n+1)
+…+(n+1) .
.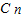 +2
+2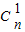 +3
+3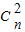 +…+(n+1)
+…+(n+1)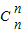 ,則有Sn=(n+1)
,則有Sn=(n+1)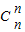 +n
+n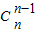 +…+3
+…+3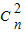 +2
+2 +
+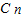 .
.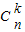 =
=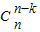 可得 2Sn=(n+2)[
可得 2Sn=(n+2)[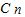 +
+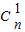 +
+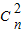 +…+
+…+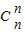 ]=(n+2)•2n-1,
]=(n+2)•2n-1,

科目:高中數學 來源: 題型:
| 1 | ||
|
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 )n展開式的各項依次記為a1(x),a2(x),a3(x)…an(x),an+1(x).設F(x)=a1(x)+2a2(x)+2a2(x)+3a3(x)…+nan(x)+(n+1)an+1(x).
)n展開式的各項依次記為a1(x),a2(x),a3(x)…an(x),an+1(x).設F(x)=a1(x)+2a2(x)+2a2(x)+3a3(x)…+nan(x)+(n+1)an+1(x).查看答案和解析>>
科目:高中數學 來源:2011年高三數學精品復習21:排列組合及二項式定理(解析版) 題型:解答題
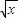 )n的展開式中第9項、第10項、第11項的二項式系數成等差數列,則n= .
)n的展開式中第9項、第10項、第11項的二項式系數成等差數列,則n= .查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com