
分析 (1)求導,求得g(x)=2lnx+2-2x+2a,(x>0)求導,根據導數與函數單調性的關系,即可求得函數g(x)的極值;
(2)由(1)可知:必然存在x0>1,使得f(x)在(1,x0)單調遞增,(x0,+∞)單調遞減,且f′(x0)=0,求得a的表達式,存在a使得f(x)max=f(x0)=0,代入即可求得x0,即可求得a的值.
解答 解:(1)函數f(x)=2xlnx-x2+2ax,(x>0)求導,g(x)=f′(x)=2lnx+2-2x+2a,(x>0)
g′(x)=$\frac{2}{x}$-2=-$\frac{2(x-1)}{x}$,(x>0)
當0<x<1時,g′(x)>0,當x>1時,g′(x)<0,
g(x)在(0,1)單調遞增;在(1,+∞)單調遞減,
∴當x=1時,取極大值,極大值為g(1)=2a,無極小值;
(2)由(1)知:f′(1)=2a>0,且f′(x)在(1,+∞)單調遞減,且x→+∞時,f′(x)<0,
則必然存在x0>1,使得f(x)在(1,x0)單調遞增,(x0,+∞)單調遞減;
且f′(x0)=2lnx0+2-2x0+2a=0,即a=-lnx0-1+x0,①
此時:當x∈[1,+∞)時,由題意知:只需要找實數a使得f(x)max=f(x0)=0,
f(x0)=2x0lnx0-x02+2ax0,將①式代入知:
f(x0)=2x0lnx0-x02+2ax0=2x0lnx0-x02+2x0(-lnx0-1+x0)=x02-2x0=0,
得到x0=2,從而a=-lnx0-1+x0=1-ln2,
∴a的值為1-ln2.
點評 本題考查導數的綜合應用,考查導數與函數單調性及極值的關系,不等式恒成立,考查轉化思想,考查計算能力,屬于中檔題.


 活力課時同步練習冊系列答案
活力課時同步練習冊系列答案 學業(yè)測評一課一測系列答案
學業(yè)測評一課一測系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -7 | B. | -1 | C. | 5 | D. | 7 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{4}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | 2 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
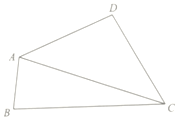 在四邊形ABCD中,∠BAD=120°,∠BCD=60°,cos∠D=-$\frac{1}{7}$,AD=DC=2,
在四邊形ABCD中,∠BAD=120°,∠BCD=60°,cos∠D=-$\frac{1}{7}$,AD=DC=2,查看答案和解析>>
科目:高中數學 來源: 題型:解答題
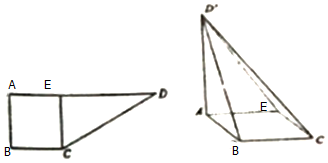
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com