
已知函數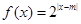 和函數
和函數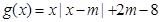 ,其中
,其中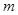 為參數,且滿足
為參數,且滿足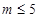 .
.
(1)若 ,寫出函數
,寫出函數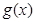 的單調區間(無需證明);
的單調區間(無需證明);
(2)若方程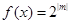 在
在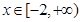 上有唯一解,求實數
上有唯一解,求實數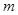 的取值范圍;
的取值范圍;
(3)若對任意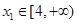 ,存在
,存在 ,使得
,使得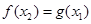 成立,求實數
成立,求實數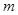 的取值范圍.
的取值范圍.
(1)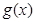 的單調增區間為
的單調增區間為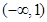 ,
,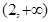 ,單調減區間為
,單調減區間為 ;(2)
;(2)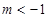 或
或 ;(3)
;(3)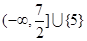 .
.
解析試題分析:(1)當 時,
時, ,由二次函數的圖像與性質可寫出函數
,由二次函數的圖像與性質可寫出函數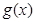 的單調區間;(2)先將
的單調區間;(2)先將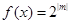 在
在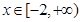 上有唯一解轉化為
上有唯一解轉化為 在
在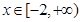 上有唯一解,進而兩邊平方得到
上有唯一解,進而兩邊平方得到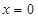 或
或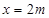 ,要使
,要使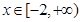 時,有唯一解,則只須
時,有唯一解,則只須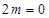 或
或 即可,問題得以解決;(3)對任意
即可,問題得以解決;(3)對任意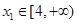 ,存在
,存在 ,使得
,使得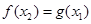 成立的意思就是
成立的意思就是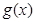 的值域應是
的值域應是 的值域的子集,然后分別針對
的值域的子集,然后分別針對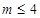 與
與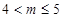 兩種情形進行討論求解,最后將這兩種情況求解出的
兩種情形進行討論求解,最后將這兩種情況求解出的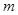 的取值范圍取并集即可.
的取值范圍取并集即可.
試題解析:(1) 時,
時, 1分
1分
函數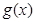 的單調增區間為
的單調增區間為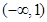 ,
,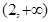 ,單調減區間為
,單調減區間為 4分
4分
(2)由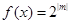 在
在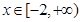 上有唯一解
上有唯一解
得 在
在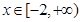 上有唯一解 5分
上有唯一解 5分
即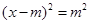 ,解得
,解得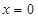 或
或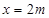 6分
6分
由題意知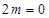 或
或
即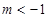 或
或
綜上,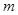 的取值范圍是
的取值范圍是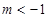 或
或 8分
8分
(3)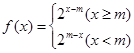
則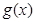 的值域應是
的值域應是 的值域的子集 9分
的值域的子集 9分
①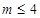 時,
時, 在
在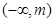 上單調遞減,
上單調遞減,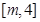 上單調遞增,故
上單調遞增,故 10分
10分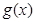 在
在 上單調遞增,故
上單調遞增,故 11分
11分
所以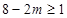 ,即
,即 12分
12分
②當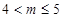 時,
時, 在
在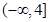 上單調遞減,故
上單調遞減,故
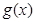 在
在 上單調遞減,
上單調遞減,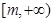 上單調遞增,故
上單調遞增,故

科目:高中數學 來源: 題型:解答題
為了保護環境,某工廠在國家的號召下,把廢棄物回收轉化為某種產品,經測算,處理成本 (萬元)與處理量
(萬元)與處理量 (噸)之間的函數關系可近似的表示為:
(噸)之間的函數關系可近似的表示為: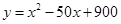 ,且每處理一噸廢棄物可得價值為
,且每處理一噸廢棄物可得價值為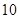 萬元的某種產品,同時獲得國家補貼
萬元的某種產品,同時獲得國家補貼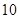 萬元.
萬元.
(1)當 時,判斷該項舉措能否獲利?如果能獲利,求出最大利潤;
時,判斷該項舉措能否獲利?如果能獲利,求出最大利潤;
如果不能獲利,請求出國家最少補貼多少萬元,該工廠才不會虧損?
(2)當處理量為多少噸時,每噸的平均處理成本最少?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某商場銷售某種商品的經驗表明,該商品每日的銷售量y(單
位:千克)與銷售價格x(單位:元/千克)滿足關系式y=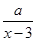 +10(x-6)2,其中3<x<6,a為常數.已知銷售價格為5元/千克時,每日可售出該商品11千克.
+10(x-6)2,其中3<x<6,a為常數.已知銷售價格為5元/千克時,每日可售出該商品11千克.
①求a的值;
②若該商品的成本為3元/千克,試確定銷售價格x的值,使商場每日銷售該商品所獲得的利潤最大.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某公司生產一種電子儀器的固定成本為20000元,每生產一臺儀器需增加投入100元,已知總收益滿足函數: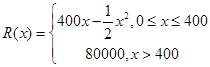 ,其中
,其中 是儀器的月產量.
是儀器的月產量.
(注:總收益=總成本+利潤)
(1)將利潤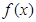 表示為月產量
表示為月產量 的函數;
的函數;
(2)當月產量 為何值時,公司所獲利潤最大?最大利潤為多少元?
為何值時,公司所獲利潤最大?最大利潤為多少元?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某廠生產某種產品的年固定成本為250萬元,每生產x千件,需另投入成本為C(x),當年產量不足80千件時,C(x)= x2+10x(萬元).當年產量不小于80千件時,C(x)=51x+
x2+10x(萬元).當年產量不小于80千件時,C(x)=51x+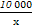 -1450(萬元).每件商品售價為0.05萬元.通過市場分析,該廠生產的商品能全部售完.
-1450(萬元).每件商品售價為0.05萬元.通過市場分析,該廠生產的商品能全部售完.
(1)寫出年利潤L(x)(萬元)關于年產量x(千件)的函數解析式.
(2)年產量為多少千件時,該廠在這一商品的生產中所獲利潤最大?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知二次函數f(x)=x2+(2a-1)x+1-2a.
(1)判斷命題“對于任意的a∈R(R為實數集),方程f(x)=1必有實數根”的真假,并寫出判斷過程.
(2)若y=f(x)在區間(-1,0)及(0, )內各有一個零點,求實數a的范圍.
)內各有一個零點,求實數a的范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某村莊擬修建一個無蓋的圓柱形蓄水池(不計厚度).設該蓄水池的底面半徑為r米,高為h米,體積為V立方米.假設建造成本僅與表面積有關,側面積的建造成本為100元/平方米,底面的建造成本為160元/平方米,該蓄水池的總建造成本為12 000π元(π為圓周率).
(1)將V表示成r的函數V(r),并求該函數的定義域;
(2)討論函數V(r)的單調性,并確定r和h為何值時該蓄水池的體積最大.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com