培優口算題卡系列答案
開心口算題卡系列答案
口算題卡河北少年兒童出版社系列答案科目：高中數學 來源： 題型：解答題
定義在[﹣1，1]上的奇函數f（x）滿足f（1）=2，且當a，b∈[﹣1，1]，a+b≠0時，有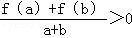
．
（1）試問函數f（x）的圖象上是否存在兩個不同的點A，B，使直線AB恰好與y軸垂直，若存在，求出A，B兩點的坐標；若不存在，請說明理由并加以證明．
（2）若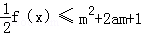
對所有x∈[﹣1，1]，a∈[﹣1，1]恒成立，求實數m的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
某公司為一家制冷設備廠設計生產某種型號的長方形薄板，其周長為4m．這種薄板須沿其對角線折疊后使用．如圖所示，ABCD(AB＞AD)為長方形薄板，沿AC折疊后AB′交DC于點P.當△ADP的面積最大時最節能，凹多邊形ACB′PD的面積最大時制冷效果最好．
(1)設AB＝xm，用x表示圖中DP的長度，并寫出x的取值范圍；
(2)若要求最節能，應怎樣設計薄板的長和寬？
(3)若要求制冷效果最好，應怎樣設計薄板的長和寬？
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
如圖,建立平面直角坐標系xOy,x軸在地平面上,y軸垂直于地平面,單位長度為1千米.某炮位于坐標原點.已知炮彈發射后的軌跡在方程y=kx-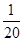
(1+k2)x2(k>0)表示的曲線上,其中k與發射方向有關.炮的射程是指炮彈落地點的橫坐標.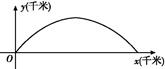
(1)求炮的最大射程;
(2)設在第一象限有一飛行物(忽略其大小),其飛行高度為3.2千米,試問它的橫坐標a不超過多少時,炮彈可以擊中它?請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
已知函數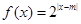
和函數
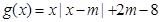，其中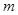
為參數，且滿足
.
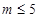（1）若
，寫出函數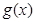
的單調區間（無需證明）；
（2）若方程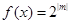
在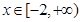
上有唯一解，求實數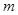的取值范圍；
（3）若對任意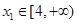
，存在
，使得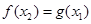
成立，求實數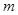的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
設函數f(x)＝ax2＋bx＋c，且f(1)＝－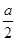
，3a＞2c＞2b，求證：
(1)a＞0，且－3＜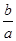
＜－
；
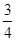(2)函數f(x)在區間(0,2)內至少有一個零點；
(3)設x1，x2是函數f(x)的兩個零點，則
≤|x1－x2|＜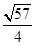
.
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
某創業投資公司擬投資開發某種新能源產品，估計能獲得10萬元到1 000萬元的投資收益．現準備制定一個對科研課題組的獎勵方案：資金y(單位：萬元)隨投資收益x(單位：萬元)的增加而增加，且獎金不超過9萬元，同時獎金不超過投資收益的20%.
(1)若建立函數y＝f(x)模型制定獎勵方案，試用數學語言表述該公司對獎勵函數f(x)模型的基本要求，并分析函數y＝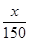
＋2是否符合公司要求的獎勵函數模型，并說明原因；
(2)若該公司采用模型函數y＝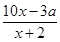
作為獎勵函數模型，試確定最小的正整數a的值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
－lg
＋lg12.5－log89·log278；
是R上的偶函數．