Question

19．設x，y滿足線性約束條件$\left\{\begin{array}{l}{2x-y+2≥0}\\{x-3y+1≤0}\\{x+y-2≤0}\end{array}\right.$，若z=ax-y（a＞0）取得最大值的最優解有數多個，則實數a的值為（　　）

• A． 2
• B． $\frac{1}{3}$
• C． $\frac{1}{2}$
• D． 3

Answer 1

分析 作出不等式對應的平面區域，利用線性規劃的知識，要使目標函數的最優解有無數個，則目標函數和其中一條直線平行，然后根據條件即可求出a的值．

解答 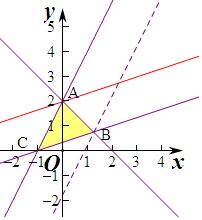解：作出不等式組對應的平面區域如圖：（陰影部分）．
由z=ax-y（a＞0）得y=ax-z，
∵a＞0，∴目標函數的斜率k=a＞0．
平移直線y=ax-z，
由圖象可知當直線y=ax-z和直線2x-y+2=0平行時，當直線經過B時，此時目標函數取得最大值時最優解只有一個，不滿足條件．
當直線y=ax-z和直線x-3y+1=0平行時，此時目標函數取得最大值時最優解有無數多個，滿足條件．
此時a=$\frac{1}{3}$．
故選：B．

點評 本題主要考查線性規劃的應用，根據目標函數的取值范圍得到目標斜率的取值關系是解決本題的關鍵，要注意使用數形結合的數學思想．