
 ×50=210,解得x=20,
×50=210,解得x=20,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:填空題
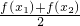 <f(
<f( ).
).查看答案和解析>>
科目:高中數學 來源: 題型:單選題
 如圖是2012年某市元旦晚會舉辦的挑戰主持人大賽上,七位評委為某選手打出的分數的莖葉統計圖,去掉一個最高分和一個最低分后,所剩數據的平均數和方差分別為
如圖是2012年某市元旦晚會舉辦的挑戰主持人大賽上,七位評委為某選手打出的分數的莖葉統計圖,去掉一個最高分和一個最低分后,所剩數據的平均數和方差分別為查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com