
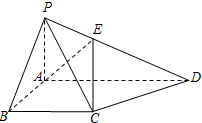
 如圖,在四棱錐P-ABCD中,底面ABCD為直角梯形,∠ABC=∠BAD=90°,且PA=AB=BC=$\frac{1}{2}$AD=1,PA⊥平面ABCD.
如圖,在四棱錐P-ABCD中,底面ABCD為直角梯形,∠ABC=∠BAD=90°,且PA=AB=BC=$\frac{1}{2}$AD=1,PA⊥平面ABCD.分析 (1)以A為坐標(biāo)原點建立空間直角坐標(biāo)系,求出$\overrightarrow{PB}$,平面PCD的法向量,即可求PB與平面PCD所成角的正弦值;
(2)假設(shè)存在E符合條件,設(shè)$\overrightarrow{PE}=λ\overrightarrow{PD}(0≤λ≤1)$,則由∠AEC=90°得,$\overrightarrow{AE}•$$\overrightarrow{CE}=2λ(2λ-1)+(1-λ{(lán))^2}=0$,列出方程,判定方程在[0,1]上是否有解即可得出結(jié)論.
解答 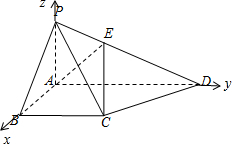 解:(1)依題意,以A為坐標(biāo)原點,分別以AB,AD,AP
解:(1)依題意,以A為坐標(biāo)原點,分別以AB,AD,AP
為x,y,z軸建立空間直角坐標(biāo)系O-xyz,則P(0,0,1),
B(1,0,0),C(1,1,0),D(0,2,0),
從而$\overrightarrow{PB}=(1,0,-1)$,$\overrightarrow{PC}=(1,1,-1)$,$\overrightarrow{PD}=(0,2,-1)$,
設(shè)平面PCD的法向量為$\overrightarrow{n}$=(a,b,c),即$\left\{\begin{array}{l}{a+b-c=0}\\{2b-c=0}\end{array}\right.$,
不妨取c=2,則b=1,a=1,
所以平面PCD的一個法向量為$\overrightarrow{n}$=(1,1,2),(4分)
此時cos<$\overrightarrow{PB}$,$\overrightarrow{n}$>=$\frac{1-2}{\sqrt{2}×\sqrt{6}}$=-$\frac{\sqrt{3}}{6}$,
所以PB與平面PCD所成角的正弦值為$\frac{{\sqrt{3}}}{6}$;(6分)
(2)設(shè)$\overrightarrow{PE}=λ\overrightarrow{PD}(0≤λ≤1)$,則E(0,2λ,1-λ),
則$\overrightarrow{CE}=(-1,2λ-1,1-λ)$,$\overrightarrow{AE}=(0,2λ,1-λ)$,
由∠AEC=90°得,$\overrightarrow{AE}•$$\overrightarrow{CE}=2λ(2λ-1)+(1-λ{(lán))^2}=0$,
化簡得,5λ2-4λ+1=0,該方程無解,
所以,棱PD上不存在一點E滿足∠AEC=90°.(10分)
點評 本題考查了空間向量的應(yīng)用,線面角的計算,屬于中檔題.


科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | $\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | $\sqrt{2}$或1 | D. | 2$\sqrt{2}$或$\sqrt{2}$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
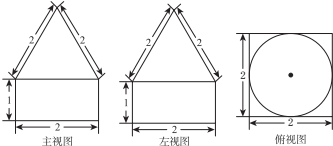
| A. | $2+\frac{{\sqrt{3}}}{3}π$ | B. | $4+\sqrt{3}π$ | C. | $\frac{4}{3}+\frac{{\sqrt{3}}}{3}π$ | D. | $4+\frac{{\sqrt{3}}}{3}π$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
 如圖,在直三棱柱ADF-BCE中,AB=BC=BE=2,CE=$2\sqrt{2}$.
如圖,在直三棱柱ADF-BCE中,AB=BC=BE=2,CE=$2\sqrt{2}$.查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
 在四棱錐V-ABCD中,底面ABCD是正方形,側(cè)面VAD是正三角形,平面VAD⊥底面ABCD.
在四棱錐V-ABCD中,底面ABCD是正方形,側(cè)面VAD是正三角形,平面VAD⊥底面ABCD.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com