
【題目】已知過拋物線y2=4x焦點F的直線l交拋物線于A、B兩點(點A在第一象限),若![]() 3
3![]() ,則直線l的斜率為( )
,則直線l的斜率為( )
A.2B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
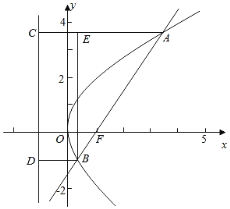
作出拋物線的準線,設A、B在l上的射影分別是C、D,連接AC、BD,過B作BE⊥AC于E.由拋物線的定義結合題中的數據,可算出Rt△ABE中,cos∠BAE![]() ,得∠BAE=60°,即直線AB的傾斜角為60°,從而得到直線AB的斜率k值.
,得∠BAE=60°,即直線AB的傾斜角為60°,從而得到直線AB的斜率k值.
作出拋物線的準線l:x=﹣1,設A、B在l上的射影分別是C、D,
連接AC、BD,過B作BE⊥AC于E.
∵![]() 3
3![]() ,∴設AF=3m,BF=m,
,∴設AF=3m,BF=m,
由點A、B分別在拋物線上,結合拋物線的定義,得AC=3m,BD=m.
因此,Rt△ABE中,cos∠BAE![]() ,得∠BAE=60°
,得∠BAE=60°
所以,直線AB的傾斜角∠AFx=60°,
得直線AB的斜率k=tan60°![]() ,
,
故選:D.


 口算題卡加應用題集訓系列答案
口算題卡加應用題集訓系列答案 綜合自測系列答案
綜合自測系列答案科目:高中數學 來源: 題型:
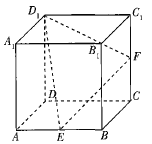
【題目】如圖,在棱長為12的正方體![]() 中,已知E,F分別為棱AB,
中,已知E,F分別為棱AB,![]() 的中點,若過點
的中點,若過點![]() ,E,F的平面截正方體
,E,F的平面截正方體![]() 所得的截面為一個多邊形,則該多邊形的周長為________,該多邊形與平面
所得的截面為一個多邊形,則該多邊形的周長為________,該多邊形與平面![]() ,ABCD的交線所成角的余弦值為________.
,ABCD的交線所成角的余弦值為________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】角谷猜想,也叫![]() 猜想,是由日本數學家角谷靜夫發現的,是指對于每一個正整數,如果它是奇數,則對它乘3再加1;如果它是偶數,則對它除以2,如此循環最終都能夠得到1.如:取
猜想,是由日本數學家角谷靜夫發現的,是指對于每一個正整數,如果它是奇數,則對它乘3再加1;如果它是偶數,則對它除以2,如此循環最終都能夠得到1.如:取![]() ,根據上述過程,得出6,3,10,5,16,8,4,2,1,共9個數.若
,根據上述過程,得出6,3,10,5,16,8,4,2,1,共9個數.若![]() ,根據上述過程得出的整數中,隨機選取兩個不同的數,則這兩個數都是偶數的概率為( )
,根據上述過程得出的整數中,隨機選取兩個不同的數,則這兩個數都是偶數的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給定下列四個命題,其中真命題是( )
A.垂直于同一直線的兩條直線相互平行
B.若一個平面內的兩條直線與另一個平面都平行,那么這兩個平面相互平行
C.垂直于同一平面的兩個平面相互平行
D.若兩個平面垂直,那么一個平面內與它們的交線不垂直的直線與另一個平面也不垂直
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年底,武漢發生“新型冠狀病毒”肺炎疫情,國家衛健委緊急部署,從多省調派醫務工作者前去支援,正值農歷春節舉家團圓之際,他們成為“最美逆行者”.武漢市從2月7日起舉全市之力入戶上門排查確診的新冠肺炎患者疑似的新冠肺炎患者無法明確排除新冠肺炎的發熱患者和確診患者的密切接觸者等“四類”人員,強化網格化管理,不落一戶不漏一人.若在排查期間,某小區有5人被確認為“確診患者的密切接觸者”,現醫護人員要對這5人隨機進行逐一“核糖核酸”檢測,只要出現一例陽性,則將該小區確定為“感染高危小區”.假設每人被確診的概率均為![]() 且相互獨立,若當
且相互獨立,若當![]() 時,至少檢測了4人該小區被確定為“感染高危小區”的概率取得最大值,則
時,至少檢測了4人該小區被確定為“感染高危小區”的概率取得最大值,則![]() ____.
____.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com