
【題目】如圖![]() ,在直角梯形
,在直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中點,
的中點,![]() 是
是![]() 與
與![]() 的交點.將
的交點.將![]() 沿
沿![]() 折起到
折起到![]() 的位置,如圖
的位置,如圖![]() .
.
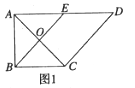
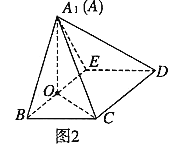
(Ⅰ)證明:![]() 平面
平面![]() ;
;
(Ⅱ)若平面![]() 平面
平面![]() ,求平面
,求平面![]() 與平面
與平面![]() 夾角的余弦值.
夾角的余弦值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】某超市舉辦酬賓活動,單次購物超過![]() 元的顧客可參與一次抽獎活動,活動規則如下:盒子中裝有大小和形狀完全相同的
元的顧客可參與一次抽獎活動,活動規則如下:盒子中裝有大小和形狀完全相同的![]() 個小球,其中
個小球,其中![]() 個紅球、
個紅球、![]() 個白球和
個白球和![]() 個黑球,從中不放回地隨機抽取
個黑球,從中不放回地隨機抽取![]() 個球,每個球被抽到的機會均等.每抽到
個球,每個球被抽到的機會均等.每抽到![]() 個紅球記
個紅球記![]() 分,每抽到
分,每抽到![]() 個白球記
個白球記![]() 分,每抽到
分,每抽到![]() 個黑球記
個黑球記![]() 分.如果抽取
分.如果抽取![]() 個球總得分
個球總得分![]() 分可獲得
分可獲得![]() 元現金,總得分低于
元現金,總得分低于![]() 分沒有現金,其余得分可獲得
分沒有現金,其余得分可獲得![]() 元現金.
元現金.
(1)設抽取![]() 個球總得分為隨機變量
個球總得分為隨機變量![]() ,求隨機變量
,求隨機變量![]() 的分布列;
的分布列;
(2)設每位顧客一次抽獎獲得現金![]() 元,求
元,求![]() 的數學期望.
的數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】德國數學家萊布尼茲(1646年-1716年)于1674年得到了第一個關于π的級數展開式,該公式于明朝初年傳入我國.在我國科技水平業已落后的情況下,我國數學家天文學家明安圖(1692年-1765年)為提高我國的數學研究水平,從乾隆初年(1736年)開始,歷時近30年,證明了包括這個公式在內的三個公式,同時求得了展開三角函數和反三角函數的6個新級數公式,著有《割圓密率捷法》一書,為我國用級數計算π開創了先河.如圖所示的程序框圖可以用萊布尼茲“關于π的級數展開式”計算π的近似值(其中P表示π的近似值),若輸入![]() ,則輸出的結果是( )
,則輸出的結果是( )
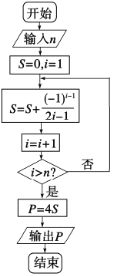
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】最新研究發現,花太多時間玩手機游戲的兒童,患多動癥的風險會加倍.青少年的大腦會很快習慣閃爍的屏幕、變幻莫測的手機游戲,一旦如此,他們在教室等視覺刺激較少的地方,就很難集中注意力.研究人員對110名年齡在7歲到8歲的兒童隨機調查,并在孩子父母的幫助下記錄了他們在1個月里玩手機游戲的習慣.同時,教師記下這些孩子出現的注意力不集中問題.統計得到下列數據:
注意力不集中 | 注意力集中 | 總計 | |
不玩手機游戲 | 20 | 40 | 60 |
玩手機游戲 | 30 | 20 | 50 |
總計 | 50 | 60 | 110 |
(1)試估計7歲到8歲不玩手機游戲的兒童中注意力集中的概率;
(2)能否在犯錯誤的概率不超過0.010的前提下認為玩手機游戲與注意力集中有關系?
附表:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.840 | 5.024 | 6.635 | 7.879 | td style="width:27.75pt; border-top-style:solid; border-top-width:0.75pt; border-left-style:solid; border-left-width:0.75pt; padding:3.38pt 5.62pt; vertical-align:middle">
 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某城市為了解游客人數的變化規律,提高旅游服務質量,收集并整理了2014年1月至2016年12月期間月接待游客量(單位:萬人)的數據,繪制了如圖所示的折線圖.根據該折線圖,下列結論錯誤的是( )
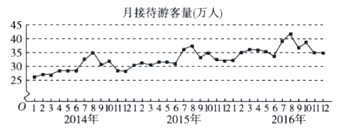
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7,8月
D.各年1月至6月的月接待游客量相對于7月至12月,波動性更小,變化比較平穩
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】小明與另外2名同學進行“手心手背”游戲,規則是:3人同時隨機等可能選擇手心或手背中的一種手勢,規定相同手勢人數多者每人得1分,其余每人得0分.現3人共進行了4次游戲,記小明4次游戲得分之和為![]() ,則
,則![]() 的期望為( )
的期望為( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
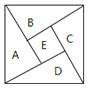
【題目】如圖為我國數學家趙爽![]() 約3世紀初
約3世紀初![]() 在為《周髀算經》作注時驗證勾股定理的示意圖,現在提供5種顏色給其中5個小區域涂色,規定每個區域只涂一種顏色,相鄰區域顏色不同,則
在為《周髀算經》作注時驗證勾股定理的示意圖,現在提供5種顏色給其中5個小區域涂色,規定每個區域只涂一種顏色,相鄰區域顏色不同,則![]() 區域涂色不相同的概率為
區域涂色不相同的概率為![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校共有6個學生餐廳,甲、乙、丙、丁四位同學每人隨機地選擇一家餐廳就餐(選擇到每個餐廳概率相同),則下列結論正確的是( )
A.四人去了四個不同餐廳就餐的概率為![]()
B.四人去了同一餐廳就餐的概率為![]()
C.四人中恰有2人去了第一餐廳就餐的概率為![]()
D.四人中去第一餐廳就餐的人數的期望為![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com