
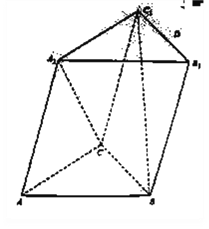
【題目】如圖,在斜三棱柱![]() 中,底面
中,底面![]() 為正三角形,面
為正三角形,面![]() ⊥面
⊥面![]() ,
, ![]() ,
,
![]() .
.
(1)求異面直線![]() 與
與![]() 所成角的余弦值;
所成角的余弦值;
(2)設![]() 為
為![]() 的中點,求面
的中點,求面![]() 與面
與面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)![]() 與
與![]() 所成角的余弦值為0. (2)
所成角的余弦值為0. (2)![]()
【解析】試題分析:(1)可設![]() ,取
,取![]() 的中點
的中點![]() ,連接
,連接![]() ,先證明
,先證明![]() ,再由面面垂直的性質可得
,再由面面垂直的性質可得![]() ,因此
,因此![]() 兩兩互相垂直.以
兩兩互相垂直.以![]() 為坐標原點,
為坐標原點, ![]() 為正交基底,建立空間直角坐標系
為正交基底,建立空間直角坐標系![]() ,分別求出
,分別求出![]() ,
, ![]() ,可得
,可得![]() ,從而得異面直線
,從而得異面直線![]() 與
與![]() 所成角的余弦值;(2)利用向量垂直數(shù)量積為零列方程組,分別求出平面
所成角的余弦值;(2)利用向量垂直數(shù)量積為零列方程組,分別求出平面![]() 的一個法向量與平面
的一個法向量與平面![]() 的一個法向量,利用空間向量夾角的余弦公式可得面
的一個法向量,利用空間向量夾角的余弦公式可得面![]() 與面
與面![]() 所成角的余弦值,進而可得正弦值.
所成角的余弦值,進而可得正弦值.
試題解析:不妨設![]() ,取
,取![]() 的中點
的中點![]() ,連接
,連接![]() ,
,
因為底面![]() 為正三角形,則
為正三角形,則![]() ,且
,且![]() ,
,
因為![]() ,所以
,所以![]() ,
,
又因為 面![]() 面
面![]() ,面
,面![]() 面
面![]()
![]() ,
, ![]() 面
面![]() ,
,
所以![]() ,因此
,因此![]() 兩兩互相垂直.以
兩兩互相垂直.以![]() 為坐標原點,
為坐標原點, ![]() 為正交基底,建立如圖所示的空間直角坐標系
為正交基底,建立如圖所示的空間直角坐標系![]() ,則
,則
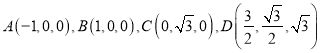 ,
,
![]() ,
,
(1)由已知得![]() ,
, ![]() ,
,
又![]() ,即
,即![]() ,所以
,所以![]() ,
,
所以![]() 與
與![]() 所成角的余弦值為0.
所成角的余弦值為0.
(2)由已知得 ,
, ![]() ,設平面
,設平面![]() 的法向量
的法向量![]()
則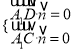 ,即
,即 ,令
,令![]() ,則
,則![]()
即平面![]() 一個法向量
一個法向量![]() ;
;
又![]() ,
, ![]() ,設平面
,設平面![]() 的法向量
的法向量![]() ,則
,則
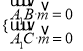 ,即
,即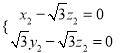 ,令
,令![]() ,則
,則![]()
即平面![]() 一個法向量
一個法向量![]() ;
;
又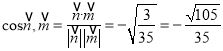 ,記面
,記面![]() 與面
與面![]() 所成的角為
所成的角為![]() ,
, ![]() ,則
,則
![]() ,所以
,所以![]()
![]() 與面
與面![]() 所成角的正弦值為
所成角的正弦值為![]() .
.
【方法點晴】本題主要考查利用空間向量求二面角,利用空間向量求異面直線所成的角,屬于難題. 空間向量解答立體幾何問題的一般步驟是:(1)觀察圖形,建立恰當?shù)目臻g直角坐標系;(2)寫出相應點的坐標,求出相應直線的方向向量;(3)設出相應平面的法向量,利用兩直線垂直數(shù)量積為零列出方程組求出法向量;(4)將空間位置關系轉化為向量關系;(5)根據(jù)定理結論求出相應的角和距離.


科目:高中數(shù)學 來源: 題型:
【題目】如圖,直線l:y=x+b (b>0),拋物線C:y2=2px(p>0),已知點P(2,2)在拋物線C上,且拋物線C上的點到直線l的距離的最小值為![]() .
.
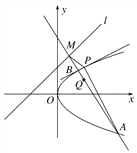
(1)求直線l及拋物線C的方程;
(2)過點Q(2,1)的任一直線(不經(jīng)過點P)與拋物線C交于A,B兩點,直線AB與直線l相交于點M,記直線PA,PB,PM的斜率分別為k1,k2,k3.問:是否存在實數(shù)λ,使得k1+k2=λk3?若存在,試求出λ的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】有一矩形硬紙板材料(厚度忽略不計),一邊![]() 長為6分米,另一邊足夠長.現(xiàn)從中截取矩形
長為6分米,另一邊足夠長.現(xiàn)從中截取矩形![]() (如圖甲所示),再剪去圖中陰影部分,用剩下的部分恰好能折卷成一個底面是弓形的柱體包裝盒(如圖乙所示,重疊部分忽略不計),其中
(如圖甲所示),再剪去圖中陰影部分,用剩下的部分恰好能折卷成一個底面是弓形的柱體包裝盒(如圖乙所示,重疊部分忽略不計),其中![]() 是以
是以![]() 為圓心、
為圓心、![]() 的扇形,且弧
的扇形,且弧![]() ,
,![]() 分別與邊
分別與邊![]() ,
, ![]() 相切于點
相切于點![]() ,
, ![]() .
.
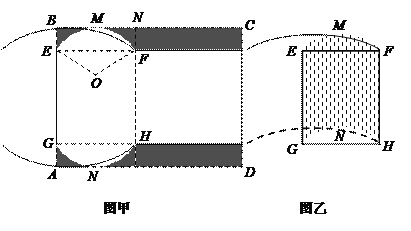
(1)當![]() 長為1分米時,求折卷成的包裝盒的容積;
長為1分米時,求折卷成的包裝盒的容積;
(2)當![]() 的長是多少分米時,折卷成的包裝盒的容積最大?
的長是多少分米時,折卷成的包裝盒的容積最大?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在直角坐標系xOy中,直線l經(jīng)過點P(2,0),其傾斜角為,在以原點O為極點,x軸非負半軸為極軸的極坐標系中(取相同的長度單位),曲線C的極坐標方程為![]() .
.
(Ⅰ)若直線l與曲線C有公共點,求傾斜角的取值范圍;
(Ⅱ)設M(x,y)為曲線C上任意一點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() 是定義在
是定義在![]() 上的偶函數(shù).當
上的偶函數(shù).當![]() 時,
時, ![]() .
.
(1) 求曲線![]() 在點
在點![]() 處的切線方程;
處的切線方程;
(2) 若關于![]() 的不等式
的不等式![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知下列命題:
①從勻速傳遞的產品生產流水線上,質檢員每30分鐘從生產流水線中抽取一件產品進行某項指標檢測,這樣的抽樣方法是系統(tǒng)抽樣;
②兩個變量的線性相關程度越強,則相關系數(shù)的值越接近于1;
③兩個分類變量![]() 與
與![]() 的觀測值
的觀測值![]() ,若
,若![]() 越小,則說明“
越小,則說明“![]() 與
與![]() 有關系”的把握程度越大;
有關系”的把握程度越大;
④隨機變量![]() ~
~![]() ,則
,則![]() .
.
其中為真命題的是__________.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知坐標平面上動點![]() 與兩個定點
與兩個定點![]() ,
, ![]() ,且
,且![]() .
.
(1)求點![]() 的軌跡方程,并說明軌跡是什么圖形;
的軌跡方程,并說明軌跡是什么圖形;
(2)記(1)中軌跡為![]() ,過點
,過點![]() 的直線
的直線![]() 被
被![]() 所截得的線段長度為8,求直線
所截得的線段長度為8,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某地區(qū)2007年至2013年農村居民家庭純收入y(單位:千元)的數(shù)據(jù)如下表:

(1)求![]() 關于
關于![]() 的線性回歸方程;
的線性回歸方程;
(2)利用(Ⅰ)中的回歸方程,分析2007年至2013年該地區(qū)農村居民家庭人均純收入的變化情況,并預測該地區(qū)2015年農村居民家庭人均純收入.
附:回歸直線的斜率和截距的最小二乘法估計公式分別為:
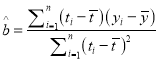 ,
, ![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
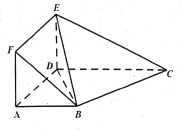
【題目】如圖,在幾何體![]() 中,四邊形
中,四邊形![]() 為矩形,四邊形
為矩形,四邊形![]() 為梯形,
為梯形, ![]() ,平面
,平面![]() 與平面
與平面![]() 垂直,且
垂直,且![]() .
.
(1)求證: ![]() 平面
平面![]() ;
;
(2)若![]() ,且平面
,且平面![]() 與平面
與平面![]() 所成銳二面角的余弦值為
所成銳二面角的余弦值為![]() ,求
,求![]() 的長.
的長.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com