
分析 (1)由直線$l:ρsin(θ-\frac{π}{4})=4$,得$\frac{\sqrt{2}}{2}ρsinθ$-$\frac{\sqrt{2}}{2}ρcosθ$=4,由此能求出直線L的直角坐標方程.
(2)由圓$C:ρ=2k•cos(θ+\frac{π}{4})(k≠0)$,得(x-$\frac{\sqrt{2}}{2}$k)2+(y+$\frac{\sqrt{2}}{2}k$)2=k2,圓C的圓心C($\frac{\sqrt{2}}{2}k$,-$\frac{\sqrt{2}}{2}k$),半徑r=|k|,由此利用直線上的點到圓C上的點的最小距離等于2,能求出k.
解答 解:(1)∵直線$l:ρsin(θ-\frac{π}{4})=4$,
∴$ρ(sinθcos\frac{π}{4}-cosθsin\frac{π}{4})$=$\frac{\sqrt{2}}{2}ρsinθ$-$\frac{\sqrt{2}}{2}ρcosθ$=4,
∴$\frac{\sqrt{2}}{2}y-\frac{\sqrt{2}}{2}x=4$.
∴整理,得:直線L的直角坐標方程為x-y+4$\sqrt{2}$=0.
(2)∵圓$C:ρ=2k•cos(θ+\frac{π}{4})(k≠0)$,
∴圓C:$ρ=2k(cosθcos\frac{π}{4}-sinθsin\frac{π}{4})$=2k×$\frac{\sqrt{2}}{2}$(cosθ-sinθ)=$\sqrt{2}k(cosθ-sinθ)$,
∴${ρ}^{2}=\sqrt{2}kρcosθ-\sqrt{2}kρsinθ$,
∴x2+y2=$\sqrt{2}kx-\sqrt{2}ky$,
即(x-$\frac{\sqrt{2}}{2}$k)2+(y+$\frac{\sqrt{2}}{2}k$)2=k2,
∴圓C的圓心C($\frac{\sqrt{2}}{2}k$,-$\frac{\sqrt{2}}{2}k$),半徑r=|k|,
∵直線上的點到圓C上的點的最小距離等于2,
∴$\frac{|\frac{\sqrt{2}}{2}k+\frac{\sqrt{2}}{2}k+4\sqrt{2}|}{\sqrt{2}}$=|k|+2,∴|k+4|=|k|+2,
解得k=-1.
點評 本題考查直線的直角坐標方程的求法,考查實數值的求法,是中檔題,解題時要認真審題,注意極坐標與直角坐標互化公式和點到直線的距離公式的合理運用.


 成功訓練計劃系列答案
成功訓練計劃系列答案 倍速訓練法直通中考考點系列答案
倍速訓練法直通中考考點系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作業本系列答案
名校作業本系列答案 輕巧奪冠周測月考直通名校系列答案
輕巧奪冠周測月考直通名校系列答案科目:高中數學 來源:2016-2017學年河北正定中學高二上月考一數學(理)試卷(解析版) 題型:解答題
執行如圖所示的程序框圖.
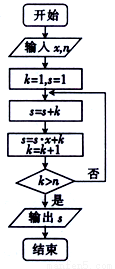
(1)若輸入的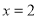 ,
,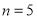 ,求輸出的
,求輸出的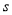 的值;
的值;
(2)若輸入的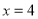 ,輸出的
,輸出的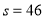 ,求輸入的
,求輸入的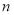 (
(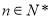 )的值.
)的值.
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
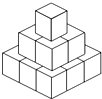 把14個棱長為1的正方體,在地面上堆疊成如圖所示的幾何體,然后將露出的表面部分染成紅色.那么紅色部分的面積為( )
把14個棱長為1的正方體,在地面上堆疊成如圖所示的幾何體,然后將露出的表面部分染成紅色.那么紅色部分的面積為( )| A. | .21 | B. | .24 | C. | .33 | D. | .37 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 銳角三角形 | B. | 直線三角形 | C. | 等腰三角形 | D. | 正三角形 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 分組 | [29.86, 29.90) | [29.90,29.94) | [29.94, 29.98) | [29.98, 30.02) | [30.02, 30.06) | [30.06, 30.10) | [30.10, 30.14) |
| 頻數 | 15 | 30 | 125 | 198 | 77 | 35 | 20 |
| 分組 | [29.86, 29.90) | [29.90, 29.94) | [29.94, 29.98) | [29.98, 30.02) | [30.02, 30.06) | [30.06, 30.10) | [30.10, 30.14) |
| 頻數 | 40 | 70 | 79 | 162 | 59 | 55 | 35 |
| 甲廠 | 乙廠 | 合計 | |
| 優質品 | |||
| 非優質品 | |||
| 合計 |
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 | |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com