【題目】已知
， 
.
（Ⅰ）討論
的單調性；
（Ⅱ）若
，求實數
的取值范圍.
【答案】（Ⅰ）詳見解析；（Ⅱ） 
.
【解析】試題分析：
（Ⅰ）由函數的解析式可得
，當
時， 
， 
在
上單調遞增；當
時，由導函數的符號可知
在
單調遞減；在
單調遞增.
（Ⅱ）構造函數
，問題轉化為
在
上恒成立，求導有
，注意到
.分類討論：當
時，不滿足題意. 當
時， 
， 
在
上單調遞增；所以
，滿足題意.
則實數
的取值范圍是
.
試題解析：
（Ⅰ）
，
當
時， 
， 
.∴
在
上單調遞增；
當
時，由
，得
.
當
時， 
；當
時， 
.
所以
在
單調遞減；在
單調遞增.
（Ⅱ）令
，
問題轉化為
在
上恒成立，
，注意到
.
當
時， 
，
，
因為
，所以
， 
，
所以存在
，使
，
當
時， 
， 
遞減，
所以
，不滿足題意.
當
時， 
，
當
時， 
， 
，
所以
， 
在
上單調遞增；所以
，滿足題意.
綜上所述： 
.
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】“過大年，吃水餃”是我國不少地方過春節的一大習俗，2018年春節前夕，
市某質檢部門隨機抽取了100包某種品牌的速凍水餃，檢測其某項質量指標．
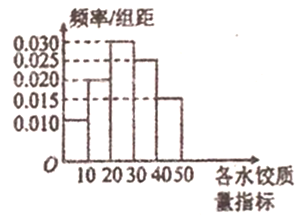
（1）求所抽取的100包速凍水餃該項質量指標值的樣本平均數
（同一組中的數據用該組區間的中點值作代表）；
（2）①由直方圖可以認為，速凍水餃的該項質量指標值
服從正態分布
，利用該正態分布，求落在
內的概率；
②將頻率視為概率，若某人從某超市購買了4包這種品牌的速凍水餃，記這4包速凍水餃中這種質量指標值位于
內的包數為
，求的分布列和數學期望.
附：①計算得所抽查的這100包速凍水餃的質量指標的標準差為
；
②若
，則
，
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某地
戶家庭的年收入
（萬元）和年飲食支出
（萬元）的統計資料如下表：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
（1）求
關于
的線性回歸方程；（結果保留到小數點后
為數字）
（2）利用（1）中的回歸方程，分析這
戶家庭的年飲食支出的變化情況，并預測該地年收入
萬元的家庭的年飲食支出.（結果保留到小數點后
位數字）
附：回歸直線的斜率和截距的最小二乘法估計公式分別為：
， 
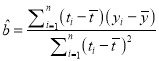查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】平面直角坐標系
中，圓
的圓心為
.已知點
，且
為圓
上的動點，線段
的中垂線交
于點
.
（Ⅰ）求點
的軌跡方程；
（Ⅱ）設點
的軌跡為曲線
，拋物線
： 
的焦點為
.
， 
是過點
互相垂直的兩條直線，直線
與曲線
交于
， 
兩點，直線
與曲線
交于
， 
兩點，求四邊形
面積的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】【2018江蘇南京師大附中、天一、海門、淮陰四校高三聯考】如圖，一只螞蟻從單位正方體
的頂點
出發，每一步（均為等可能性的）經過一條邊到達另一頂點，設該螞蟻經過
步回到點的概率
．
（I）分別寫出
的值；
（II）設頂點出發經過步到達點
的概率為
，求
的值；
（III）求．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，已知四棱錐
， 
平面
，底面
中， 
， 
，且
， 
為
的中點．
（1）求證：平面
平面
；
（2）問在棱
上是否存在點
，使
平面
，若存在，請求出二面角
的余弦值；若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某城市為鼓勵人們綠色出行，乘坐地鐵，地鐵公司決定按照乘客經過地鐵站的數量實施分段優惠政策，不超過
站的地鐵票價如下表：
乘坐站數 |
|
|
|
票價（元） |
|
|
|
現有甲、乙兩位乘客同時從起點乘坐同一輛地鐵，已知他們乘坐地鐵都不超過
站.甲、乙乘坐不超過
站的概率分別為
， 
；甲、乙乘坐超過
站的概率分別為
， 
.
（1）求甲、乙兩人付費相同的概率；
（2）設甲、乙兩人所付費用之和為隨機變量
，求
的分布列和數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
