
【題目】某個部件由三個元件按如圖所示的方式連接而成,元件1或元件2正常工作,且元件3正常工作,則部件正常工作.設三個電子元件的使用壽命(單位:時)均服從正態分布N(1000,502),且各個元件能否正常工作相互獨立,那么該部件的使用壽命超過1000小時的概率為( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】為了了解某校學生喜歡吃零食是否與性別有關,隨機對此校100人進行調查,得到如下的列表:已知在全部100人中隨機抽取1人,抽到不喜歡吃零食的學生的概率為![]() .
.
喜歡吃零食 | 不喜歡吃零食辣 | 合計 | |
男生 | 10 | ||
女生 | 20 | ||
合計 | 100 |
(Ⅰ)請將上面的列表補充完整;
(Ⅱ)是否有99.9%以上的把握認為喜歡吃零食與性別有關?說明理由.
下面的臨界值表供參考:![]() ,其中
,其中![]()
| 0.010 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)=|2x-1|-|x+1|.
(1)將f(x)的解析式寫成分段函數的形式,并作出其圖象;
(2)若a+b=1,對a,b∈(0,+∞),![]() +
+![]() ≥3f(x)恒成立,求x的取值范圍.
≥3f(x)恒成立,求x的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某火鍋店為了了解氣溫對營業額的影響,隨機記錄了該店1月份其中5天的日營業額y(單位:萬元)與該地當日最低氣溫x(單位:℃)的數據,如下表:
![]()
(1)求y關于x的線性回歸方程![]() =
=![]() x+
x+![]() ;
;
(2)判斷y與x之間是正相關還是負相關,若該地1月份某天的最低氣溫為6 ℃,用所求回歸方程預測該店當日的營業額;
(3)設該地1月份的日最低氣溫X~N(μ,σ2),其中μ近似為樣本平均數![]() ,σ2近似為樣本方差s2,求P(3.8<X≤13.4).
,σ2近似為樣本方差s2,求P(3.8<X≤13.4).
附:①回歸方程![]() 中,
中,![]() =
=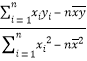 ,
,![]() =
=![]() ﹣
﹣![]() .
.
②![]() ≈3.2,
≈3.2,![]() ≈1.8.若X~N(μ,σ2),則P(μ-σ<X≤μ+σ)=0.682 7,P(μ-2σ<X≤μ+2σ)=0.954 5.
≈1.8.若X~N(μ,σ2),則P(μ-σ<X≤μ+σ)=0.682 7,P(μ-2σ<X≤μ+2σ)=0.954 5.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的上頂點為
的上頂點為![]() ,且離心率為
,且離心率為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設![]() 是曲線
是曲線![]() 上的動點,
上的動點,![]() 關于
關于![]() 軸的對稱點為
軸的對稱點為![]() ,點
,點![]() ,直線
,直線![]() 與曲線
與曲線![]() 的另一個交點為
的另一個交點為![]() (
(![]() 與
與![]() 不重合),過
不重合),過![]() 作直線
作直線![]() ,垂足為
,垂足為![]() ,是否存在定點
,是否存在定點![]() ,使
,使![]() 為定值?若存在求出
為定值?若存在求出![]() 的坐標,不存在說明理由?
的坐標,不存在說明理由?

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在航天員進行的一項太空實驗中,要先后實施6個程序,其中程序![]() 只能出現在第一步或最后一步,程序
只能出現在第一步或最后一步,程序![]() 實施時必須相鄰,請問實驗順序的編排方法共有 ( )
實施時必須相鄰,請問實驗順序的編排方法共有 ( )
A. ![]() 種 B.
種 B. ![]() 種 C.
種 C. ![]() 種 D.
種 D. ![]() 種
種
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面ABCD為平行四邊形,PA⊥底面ABCD,
中,底面ABCD為平行四邊形,PA⊥底面ABCD,![]() ,
,![]() ,
,![]() ,
,![]() .
.
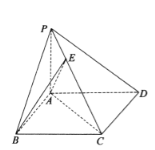
(1)求證:平面PCA⊥平面PCD;
(2)設E為側棱PC上的一點,若直線BE與底面ABCD所成的角為45°,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,橢圓
中,橢圓![]() 經過點
經過點![]() ,離心率為
,離心率為![]() . 已知過點
. 已知過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點.
兩點.

(1)求橢圓![]() 的方程;
的方程;
(2)試問![]() 軸上是否存在定點
軸上是否存在定點![]() ,使得
,使得![]() 為定值.若存在,求出點
為定值.若存在,求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com