
分析 (Ⅰ)利用二倍角公式、輔助角公式得到:f(x)=$\sqrt{2}$sin(2x+$\frac{π}{4}$),結(jié)合正弦函數(shù)的性質(zhì)求f(x)的最小正周期和最大值;
(Ⅱ)將f(θ+$\frac{π}{8}$)=$\frac{\sqrt{2}}{3}$代入(Ⅰ)中的函數(shù)解析式,求得cos2θ=$\frac{1}{3}$,根據(jù)θ為銳角來求sin2θ的值.
解答 解:(Ⅰ)f(x)=cos2x-sin2x+sin2x
=cos2x+sin2x
=$\sqrt{2}$($\frac{\sqrt{2}}{2}$cos2x+$\frac{\sqrt{2}}{2}$sin2x)
=$\sqrt{2}$sin(2x+$\frac{π}{4}$),
∴f(x)的最小正周期是:$\frac{2π}{2}$=π,最大值是$\sqrt{2}$,此時x=kπ+$\frac{π}{8}$,k∈Z.
(Ⅱ)∵f(θ+$\frac{π}{8}$)=$\frac{\sqrt{2}}{3}$,
∴$\sqrt{2}$sin(2θ+$\frac{π}{2}$)=$\frac{\sqrt{2}}{3}$,
∴cos2θ=$\frac{1}{3}$,
∵θ為銳角,即0<θ<$\frac{π}{2}$,
∴0<2θ<π,
∴sin2θ=$\sqrt{1-co{s}^{2}2θ}$=$\frac{2\sqrt{2}}{3}$.
點評 本題主要考查三角函數(shù)的圖象和性質(zhì),利用三角函數(shù)公式將函數(shù)進行化簡是解決本題的關(guān)鍵.


 黃岡經(jīng)典趣味課堂系列答案
黃岡經(jīng)典趣味課堂系列答案 啟東小題作業(yè)本系列答案
啟東小題作業(yè)本系列答案科目:高中數(shù)學 來源: 題型:選擇題
| X | 0 | 1 |
| p | 0.3 | 0.7 |
| A. | a=10,b=3 | B. | a=3,b=10 | C. | a=100,b=-60 | D. | a=60,b=-100 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:選擇題
| A. | (-∞,4] | B. | (-∞,4) | C. | (4,+∞) | D. | [4,+∞) |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:選擇題
| A. | $\frac{1}{9}$ | B. | $\frac{2}{9}$ | C. | $\frac{4}{9}$ | D. | $\frac{26}{27}$ |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
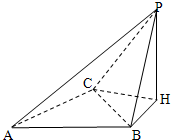 如圖,在四面體P-ABC,底面ABC是邊長為1的正三角形,AB⊥BP,點P在底面ABC上的射影為H,BH=$\frac{\sqrt{3}}{3}$,平面ACP與平面PBH所成的銳二面角的余弦值為$\frac{\sqrt{6}}{3}$.
如圖,在四面體P-ABC,底面ABC是邊長為1的正三角形,AB⊥BP,點P在底面ABC上的射影為H,BH=$\frac{\sqrt{3}}{3}$,平面ACP與平面PBH所成的銳二面角的余弦值為$\frac{\sqrt{6}}{3}$.查看答案和解析>>
科目:高中數(shù)學 來源: 題型:選擇題

| A. | $\frac{16\sqrt{2}}{3}$cm3 | B. | $\frac{32}{3}$cm3 | C. | 16$\sqrt{2}$cm3 | D. | 32cm3 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com