
已知函數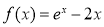 ,
,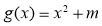 (
(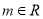 )
)
(1)對于函數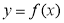 中的任意實數x,在
中的任意實數x,在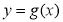 上總存在實數
上總存在實數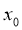 ,使得
,使得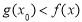 成立,求實數
成立,求實數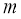 的取值范圍
的取值范圍
(2)設函數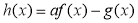 ,當
,當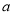 在區間
在區間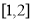 內變化時,
內變化時,
(1)求函數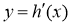
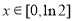 的取值范圍;
的取值范圍;
(2)若函數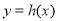
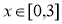 有零點,求實數m的最大值.
有零點,求實數m的最大值.
(1)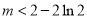 ;(2)(1)
;(2)(1)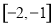 ;(2)
;(2)
【解析】
試題分析:(1)分析可知原命題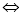
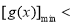
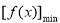 ,分別求導令導數等于0,討論導數的正負,導數大于0得增區間,導數小于0得減區間,再根據單調性求最值。(2)(1)
,分別求導令導數等于0,討論導數的正負,導數大于0得增區間,導數小于0得減區間,再根據單調性求最值。(2)(1)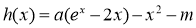 ,先求導得
,先求導得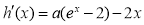 ,可看成關于
,可看成關于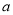 的一次函數,因為
的一次函數,因為 可得
可得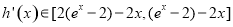 ,即
,即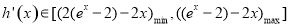 用導數討論
用導數討論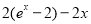 和
和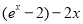 的單調性,用單調性求其最值。從而可得
的單調性,用單調性求其最值。從而可得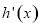 得范圍。(2)
得范圍。(2)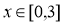 時函數
時函數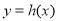 有零點,說明存在
有零點,說明存在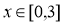 使
使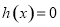 。由(1)可知
。由(1)可知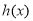 在
在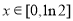 為單調遞減函數,所以函數
為單調遞減函數,所以函數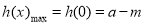 ,同(1)可得
,同(1)可得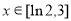 時
時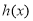 的最大值是
的最大值是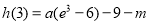 ,比較
,比較 和
和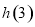 的大小得函數
的大小得函數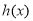 的最大值從可得
的最大值從可得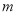 的最大值。
的最大值。
試題解析:(1)原命題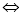
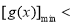
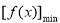 ,先求函數
,先求函數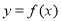 的最小值,令
的最小值,令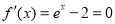 ,得
,得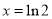 .當
.當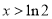 時,
時,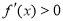 ;當
;當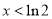 時,
時,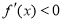 ,故當
,故當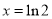 時,
時,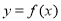 取得極(最)小值,其最小值為
取得極(最)小值,其最小值為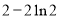 ;而函數
;而函數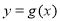 的最小值為m,故當
的最小值為m,故當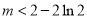 時,結論成立
時,結論成立
(2)(1):由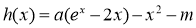 ,可得
,可得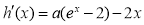 ,把
,把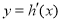 這個函數看成是關于
這個函數看成是關于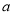 的一次函數,(1)當
的一次函數,(1)當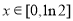 時,
時,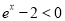 ,因為
,因為 ,故
,故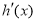 的值在區間
的值在區間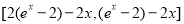 上變化,令
上變化,令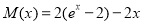 ,
,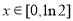 ,則
,則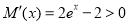 ,
,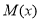 在
在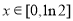 為增函數,故
為增函數,故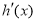 在
在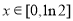 最小值為
最小值為 ,又令
,又令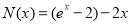 ,同樣可求得
,同樣可求得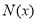 在
在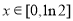 的最大值
的最大值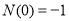 ,所以函數
,所以函數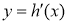 在
在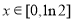 的值域為
的值域為 。
。
(2)(2)當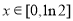 時,
時,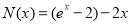 的最大值
的最大值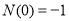 ,故對任意
,故對任意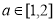 ,
,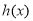 在
在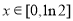 均為單調遞減函數,所以函數
均為單調遞減函數,所以函數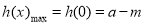
當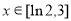 時,因為
時,因為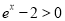 ,
,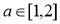 ,故
,故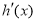 的值在區間
的值在區間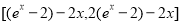 上變化,此時,對于函數
上變化,此時,對于函數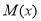 ,存在
,存在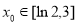 ,
,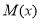 在
在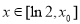 單調遞減,在
單調遞減,在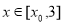 單調遞增,所以,
單調遞增,所以,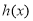 在
在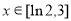 的最大值為
的最大值為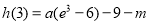 ,因為
,因為 ,
,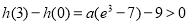 ,所以
,所以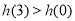 ,故
,故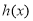 的最大值是
的最大值是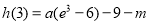 ,又因為
,又因為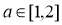 ,故當函數
,故當函數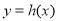 有零點時,實數m的最大值是
有零點時,實數m的最大值是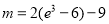
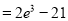 .
.
考點:用導數研究函數的單調性。


 學練快車道快樂假期暑假作業新疆人民出版社系列答案
學練快車道快樂假期暑假作業新疆人民出版社系列答案 浙大優學小學年級銜接導與練浙江大學出版社系列答案
浙大優學小學年級銜接導與練浙江大學出版社系列答案 小學暑假作業東南大學出版社系列答案
小學暑假作業東南大學出版社系列答案科目:高中數學 來源:2013-2014學年湖北省天門市畢業生四月調研考試理科數學試卷(解析版) 題型:選擇題
函數 的零點所在區間為( )
的零點所在區間為( )
A.(0,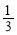 ) B.(
) B.(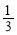 ,
,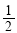 ) C.(
) C.(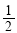 ,1) D.(1,2)
,1) D.(1,2)
查看答案和解析>>
科目:高中數學 來源:2013-2014學年湖北省七市(州)高三年級聯合考試理科數學試卷(解析版) 題型:選擇題
已知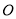 為坐標原點,
為坐標原點,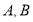 兩點的坐標均滿足不等式組
兩點的坐標均滿足不等式組 設
設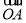 與
與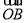 的夾角為
的夾角為
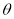 ,則
,則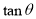 的最大值為 ( )
的最大值為 ( )
A.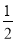 B.
B.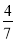 C.
C.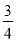 D.
D.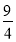
查看答案和解析>>
科目:高中數學 來源:2013-2014學年湖北省七市(州)高三年級聯合考試文科數學試卷(解析版) 題型:選擇題
萊因德紙草書》是世界上最古老的數學著作之一,書中有這樣的一道題目:把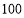 個面包分給
個面包分給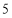 個人,使每人所得成等差數列,且使較大的三份之和的
個人,使每人所得成等差數列,且使較大的三份之和的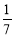 是較小的兩份之和,則最小的
是較小的兩份之和,則最小的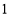 份為( )
份為( )
A.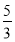 B.
B.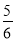 C.
C.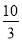 D.
D.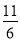
查看答案和解析>>
科目:高中數學 來源:2013-2014學年浙江省高三高考模擬沖刺卷(提優卷)(二)理科數學試卷(解析版) 題型:填空題
已知函數
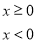 ,若關于
,若關于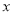 的方程
的方程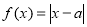 有三個不同的實根,則實數
有三個不同的實根,則實數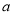 的取值范圍是_.
的取值范圍是_.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年浙江省高三高考模擬沖刺卷(提優卷)(二)理科數學試卷(解析版) 題型:選擇題
正四面體ABCD,線段AB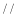 平面
平面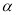 ,E,F分別是線段AD和BC的中點,當正四面體繞以AB為軸旋轉時,則線段AB與EF在平面
,E,F分別是線段AD和BC的中點,當正四面體繞以AB為軸旋轉時,則線段AB與EF在平面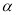 上的射影所成角余弦值的范圍是( )
上的射影所成角余弦值的范圍是( )
A. [0,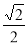 ] B.[
] B.[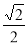 ,1] C.[
,1] C.[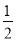 ,1] D.[
,1] D.[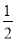 ,
,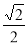 ]
]
查看答案和解析>>
科目:高中數學 來源:2013-2014學年浙江省高三高考模擬沖刺卷(提優卷)(三)文科數學試卷(解析版) 題型:解答題
(本小題滿分14分)設函數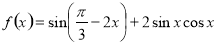
求函數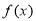 的周期和單調遞增區間;
的周期和單調遞增區間;
設A,B,C為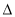 ABC的三個內角,若AB=1,
ABC的三個內角,若AB=1, 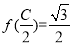 ,
,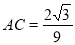 ,求sinB的值.
,求sinB的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com