
【題目】【2015高考天津,文20】已知函數(shù)![]()
(I)求![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(II)設(shè)曲線![]() 與
與![]() 軸正半軸的交點(diǎn)為P,曲線在點(diǎn)P處的切線方程為
軸正半軸的交點(diǎn)為P,曲線在點(diǎn)P處的切線方程為![]() ,求證:對于任意的正實(shí)數(shù)
,求證:對于任意的正實(shí)數(shù)![]() ,都有
,都有![]() ;
;
(III)若方程![]() 有兩個正實(shí)數(shù)根
有兩個正實(shí)數(shù)根![]() 且
且![]() ,求證:
,求證:![]() .
.
【答案】(I)![]() 的單調(diào)遞增區(qū)間是
的單調(diào)遞增區(qū)間是![]() ,單調(diào)遞減區(qū)間是
,單調(diào)遞減區(qū)間是![]() ;(II)見試題解析;(III)見試題解析.
;(II)見試題解析;(III)見試題解析.
【解析】
(I)由![]() ,可得
,可得![]() 的單調(diào)遞增區(qū)間是
的單調(diào)遞增區(qū)間是![]() ,單調(diào)遞減區(qū)間是
,單調(diào)遞減區(qū)間是![]() ;(II)
;(II)![]() ,
,![]() ,證明
,證明![]() 在
在![]() 單調(diào)遞增,在
單調(diào)遞增,在![]() 單調(diào)遞減,所以對任意的實(shí)數(shù)x,
單調(diào)遞減,所以對任意的實(shí)數(shù)x,![]() ,對于任意的正實(shí)數(shù)
,對于任意的正實(shí)數(shù)![]() ,都有
,都有![]() ;(III)設(shè)方程
;(III)設(shè)方程![]() 的根為
的根為![]() ,可得
,可得![]() ,由
,由![]() 在
在![]() 單調(diào)遞減,得
單調(diào)遞減,得![]() ,所以
,所以![]() .設(shè)曲線
.設(shè)曲線![]() 在原點(diǎn)處的切線為
在原點(diǎn)處的切線為![]() 方程
方程![]() 的根為
的根為![]() ,可得
,可得![]() ,由
,由![]() 在在
在在![]() 單調(diào)遞增,且
單調(diào)遞增,且![]() ,可得
,可得![]() 所以
所以![]() .
.
試題解析:(I)由![]() ,可得
,可得![]() ,當(dāng)
,當(dāng)![]() ,即
,即![]() 時,函數(shù)
時,函數(shù)![]() 單調(diào)遞增;當(dāng)
單調(diào)遞增;當(dāng)![]() ,即
,即![]() 時,函數(shù)
時,函數(shù)![]() 單調(diào)遞減.所以函數(shù)
單調(diào)遞減.所以函數(shù)![]() 的單調(diào)遞增區(qū)間是
的單調(diào)遞增區(qū)間是![]() ,單調(diào)遞減區(qū)間是
,單調(diào)遞減區(qū)間是![]() .
.
(II)設(shè)![]() ,則
,則![]() ,
,![]() 曲線
曲線![]() 在點(diǎn)P處的切線方程為
在點(diǎn)P處的切線方程為![]() ,即
,即![]() ,令
,令![]() 即
即![]() 則
則![]() .
.
由于![]() 在
在![]() 單調(diào)遞減,故
單調(diào)遞減,故![]() 在
在![]() 單調(diào)遞減,又因?yàn)?/span>
單調(diào)遞減,又因?yàn)?/span>![]() ,所以當(dāng)
,所以當(dāng)![]() 時,
時,![]() ,所以當(dāng)
,所以當(dāng)![]() 時,
時,![]() ,所以
,所以![]() 在
在![]() 單調(diào)遞增,在
單調(diào)遞增,在![]() 單調(diào)遞減,所以對任意的實(shí)數(shù)x,
單調(diào)遞減,所以對任意的實(shí)數(shù)x,![]() ,對于任意的正實(shí)數(shù)
,對于任意的正實(shí)數(shù)![]() ,都有
,都有![]() .
.
(III)由(II)知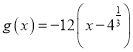 ,設(shè)方程
,設(shè)方程![]() 的根為
的根為![]() ,可得
,可得![]() ,因?yàn)?/span>
,因?yàn)?/span>![]() 在
在![]() 單調(diào)遞減,又由(II)知
單調(diào)遞減,又由(II)知![]() ,所以
,所以![]() .類似的,設(shè)曲線
.類似的,設(shè)曲線![]() 在原點(diǎn)處的切線為
在原點(diǎn)處的切線為![]() 可得
可得![]() ,對任意的
,對任意的![]() ,有
,有![]() 即
即![]() .設(shè)方程
.設(shè)方程![]() 的根為
的根為![]() ,可得
,可得![]() ,因?yàn)?/span>
,因?yàn)?/span>![]() 在
在![]() 單調(diào)遞增,且
單調(diào)遞增,且![]() ,因此,
,因此,![]() 所以
所以![]() .
.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]()
(Ⅰ)求函數(shù)![]() 在
在![]() 上的最小值;
上的最小值;
(Ⅱ)設(shè)函數(shù)![]() ,若函數(shù)
,若函數(shù)![]() 的零點(diǎn)有且只有一個,求實(shí)數(shù)
的零點(diǎn)有且只有一個,求實(shí)數(shù)![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(本小題滿分12分)某公司為了解廣告投入對銷售收益的影響,在若干地區(qū)各投入![]() 萬元廣告費(fèi)用,并將各地的銷售收益(單位:萬元)繪制成如圖所示的頻率分布直方圖.由于工作人員操作失誤,橫軸的數(shù)據(jù)丟失,但可以確定橫軸是從
萬元廣告費(fèi)用,并將各地的銷售收益(單位:萬元)繪制成如圖所示的頻率分布直方圖.由于工作人員操作失誤,橫軸的數(shù)據(jù)丟失,但可以確定橫軸是從![]() 開始計數(shù)的.
開始計數(shù)的.


(Ⅰ)根據(jù)頻率分布直方圖計算圖中各小長方形的寬度;
(Ⅱ)該公司按照類似的研究方法,測得另外一些數(shù)據(jù),并整理得到上表:表中的數(shù)據(jù)顯示![]() 與
與![]() 之間存在線性相關(guān)關(guān)系,求
之間存在線性相關(guān)關(guān)系,求![]() 關(guān)于
關(guān)于![]() 的回歸方程;
的回歸方程;
(Ⅲ)若廣告投入![]() 萬元時,實(shí)際銷售收益為
萬元時,實(shí)際銷售收益為![]() .
.![]() 萬元,求殘差
萬元,求殘差![]() .
.
![]()
 附:
附:
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】有甲、乙兩種商品,經(jīng)營銷售這兩種商品所得的利潤依次為M萬元和N萬元,它們與投入資金![]() 萬元的關(guān)系可由經(jīng)驗(yàn)公式給出:M=
萬元的關(guān)系可由經(jīng)驗(yàn)公式給出:M=![]() ,N=
,N=![]() (
(![]() ≥1).今有8萬元資金投入經(jīng)營甲、乙兩種商品,且乙商品至少要求投資1萬元,
≥1).今有8萬元資金投入經(jīng)營甲、乙兩種商品,且乙商品至少要求投資1萬元,
設(shè)投入乙種商品的資金為![]() 萬元,總利潤
萬元,總利潤![]() ;
;
(2)為獲得最大利潤,對甲、乙兩種商品的資金投入分別是多少?共能獲得多大利潤?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在四棱錐![]() 中,
中,![]() ,
,![]() ,
,![]() 和
和![]() 都是邊長為2的等邊三角形,設(shè)
都是邊長為2的等邊三角形,設(shè)![]() 在底面
在底面![]() 的射影為
的射影為![]() .
.
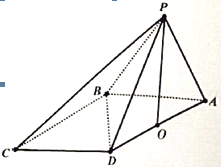
(1)求證:![]() 是
是![]() 中點(diǎn);
中點(diǎn);
(2)證明:![]() ;
;
(3)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知四邊形![]() 為直角梯形,
為直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 為
為![]() 中點(diǎn),
中點(diǎn),![]() ,
,![]() 與
與![]() 交于點(diǎn)
交于點(diǎn)![]() ,沿
,沿![]() 將四邊形
將四邊形![]() 折起,連接
折起,連接![]() .
.
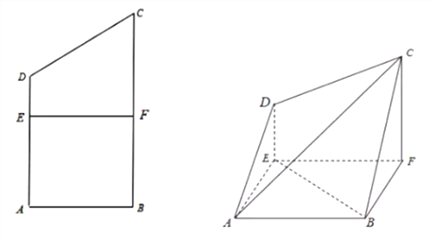
(1)求證:![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() .
.
(I)求二面角![]() 的平面角的大小;
的平面角的大小;
(II)線段![]() 上是否存在點(diǎn)
上是否存在點(diǎn)![]() ,使
,使![]() 平面
平面![]() ,若存在,求出
,若存在,求出![]() 的值,若不存在,請說明理由.
的值,若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(2016·哈爾濱高二檢測)如圖,下列四個幾何體中,它們的三視圖(正視圖、俯視圖、側(cè)視圖)有且僅有兩個相同,而另一個不同的兩個幾何體是________.


(1)棱長為2的正方體 (2)底面直徑和高均為2的圓柱

(3)底面直徑和高
均為2的圓錐
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
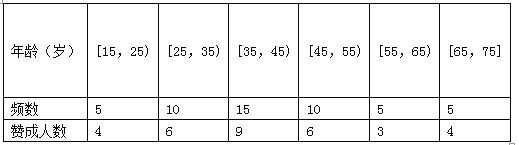
【題目】私家車的尾氣排放是造成霧霾天氣的重要因素之一,因此在生活中我們應(yīng)該提倡低碳生活,少開私家車,盡量選擇綠色出行方式,為預(yù)防霧霾出一份力.為此,很多城市實(shí)施了機(jī)動車車尾號限行,我市某報社為了解市區(qū)公眾對“車輛限行”的態(tài)度,隨機(jī)抽查了50人,將調(diào)查情況進(jìn)行整理后制成下表:
(Ⅰ)完成被調(diào)查人員的頻率分布直方圖;
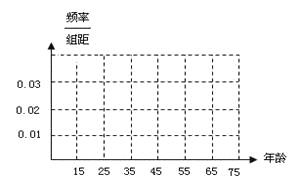
(Ⅱ)若從年齡在[15,25),[25,35)的被調(diào)查者中各隨機(jī)選取2人進(jìn)行追蹤調(diào)查,求恰有2人不贊成的概率;
(Ⅲ)在(Ⅱ)的條件下,再記選中的4人中不贊成“車輛限行”的人數(shù)為![]() ,求隨機(jī)變量
,求隨機(jī)變量![]() 的分布列和數(shù)學(xué)期望.
的分布列和數(shù)學(xué)期望.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com