
| A. | 奇函數,且在(0,1)上是增函數 | B. | 奇函數,且在(0,1)上是減函數 | ||
| C. | 偶函數,且在(0,1)上是增函數 | D. | 偶函數,且在(0,1)上是減函數 |
分析 先求出函數的定義域,判斷函數的奇偶性即可得到結論.
解答 解:要使函數f(x)有意義,則$\left\{\begin{array}{l}{1-x>0}\\{1+x>0}\end{array}\right.$,即$\left\{\begin{array}{l}{x<1}\\{x>-1}\end{array}\right.$,即-1<x<1,
則函數的定義域為(-1,1),
則f(-x)=lg(1+x)+lg(1-x)=f(x),
故函數f(x)是偶函數,
當0<x<1,y=lg(1-x)+lg(1+x)=lg(1-x)(1+x)=lg(1-x2),
當0<x<1時,函數y=1-x2為減函數,而y=lgt為增函數,
則函數y=lg(1-x2)為減函數,
故選:D
點評 本題主要考查函數奇偶性和單調性的判斷,根據函數奇偶性的定義以及復合函數單調性之間的關系是解決本題的關鍵.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
| 滿意度評分分組 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) |
| 頻數 | |||||
| 頻率 |

| 滿意度評分 | 低于70分 | 70分到89分 | 不低于90分 |
| 滿意度等級 | 不滿意 | 滿意 | 非常滿意 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $20\sqrt{6}$ | B. | 75 | C. | 51 | D. | 49 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
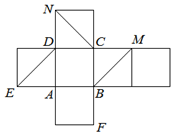 如圖是正方體的平面展開圖.在這個正方體中,
如圖是正方體的平面展開圖.在這個正方體中,| A. | ①②③④ | B. | ②④ | C. | ②③④ | D. | ②③ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-∞,0] | B. | (-∞,1] | C. | (-∞,2] | D. | (-∞,3] |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
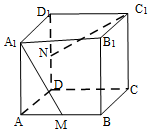 已知正方體ABCD-A1B1C1D1中,M,N分別為棱AB,DD1的中點,異面直線A1M和C1N所成的角為( )
已知正方體ABCD-A1B1C1D1中,M,N分別為棱AB,DD1的中點,異面直線A1M和C1N所成的角為( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com