
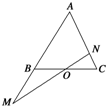
 如圖所示,在△ABC中,點O是BC的中點,過點O的直線分別交直線AB,AC于不同的兩點M,N,若$\overrightarrow{AB}$=m$\overrightarrow{AM}$,$\overrightarrow{AC}$=n$\overrightarrow{AN}$ (m,n>0),則m2+n的范圍為[$\frac{7}{4}$,4).
如圖所示,在△ABC中,點O是BC的中點,過點O的直線分別交直線AB,AC于不同的兩點M,N,若$\overrightarrow{AB}$=m$\overrightarrow{AM}$,$\overrightarrow{AC}$=n$\overrightarrow{AN}$ (m,n>0),則m2+n的范圍為[$\frac{7}{4}$,4). 分析 用$\overrightarrow{AM},\overrightarrow{AN}$表示出$\overrightarrow{AO}$,根據M,O,N三點共線得出m,n的關系,從而得出m2+n關于m的二次函數,求出m的范圍,利用二次函數的性質求出范圍.
解答 解:∵O是BC的中點,∴$\overrightarrow{AO}$=$\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AC}$=$\frac{m}{2}\overrightarrow{AM}+\frac{n}{2}\overrightarrow{AN}$,
∵M,O,N三點共線,
∴$\frac{m}{2}+\frac{n}{2}=1$,即n=2-m.
∴m2+n=m2-m+2=(m-$\frac{1}{2}$)2+$\frac{7}{4}$,
∵m>0,n>0,即$\left\{\begin{array}{l}{m>0}\\{2-m>0}\end{array}\right.$,
∴0<m<2.
令f(m)=(m-$\frac{1}{2}$)2+$\frac{7}{4}$,
∴當m=$\frac{1}{2}$時,f(m)取得最小值$\frac{7}{4}$,
當m=2時,f(m)取得最大值4.
∴$\frac{7}{4}≤f(m)<4$.
故答案為:$[{\frac{7}{4},4})$.
點評 本題考查了平面向量的基本定理,二次函數的性質,屬于中檔題.


 新思維假期作業寒假吉林大學出版社系列答案
新思維假期作業寒假吉林大學出版社系列答案科目:高中數學 來源: 題型:填空題
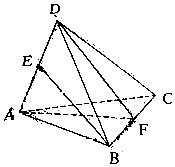 如圖,在空間四邊形ABCD中,AB,BC,CD,DA的長和兩條對角線AC,BD都相等,且E為AD的中點,F為BC的中點,則直線BE和平面ADF所成的角的正弦值為$\frac{\sqrt{3}}{3}$.
如圖,在空間四邊形ABCD中,AB,BC,CD,DA的長和兩條對角線AC,BD都相等,且E為AD的中點,F為BC的中點,則直線BE和平面ADF所成的角的正弦值為$\frac{\sqrt{3}}{3}$.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | c<a<b | B. | a<b<c | C. | b<a<c | D. | a<c<b |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{2}{3}$ | D. | $-\frac{1}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
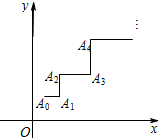 一青蛙從點A0(x0,y0)開始依次水平向右和豎直向上跳動,其落點坐標依次是Ai(xi,yi)(i∈N*),(如圖,A0(x0,y0)的坐標以已知條件為準),Sn表示青蛙從點A0到點An所經過的路程.
一青蛙從點A0(x0,y0)開始依次水平向右和豎直向上跳動,其落點坐標依次是Ai(xi,yi)(i∈N*),(如圖,A0(x0,y0)的坐標以已知條件為準),Sn表示青蛙從點A0到點An所經過的路程.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com