證明f(x)=3x2+2在區間[0,+∞)上是增函數.
【答案】
分析:在要求證的區間內任取兩個自變量x
1,x
2,規定大小后把對應的函數值作差,因式分解后判斷差式的符號,從而得到對應函數值的大小,然后利用增函數的概念得到證明.
解答:證明:設x
1,x
2∈[0,+∞),且x
1<x
2,
則
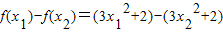
=
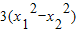
=3(x
1+x
2)(x
1-x
2).
∵x
1,x
2∈[0,+∞),且x
1<x
2,
∴x
1+x
2>0,x
1-x
2<0.
∴3(x
1+x
2)(x
1-x
2)<0.
即f(x
1)-f(x
2)<0.
f(x
1)<f(x
2).
所以f(x)=3x
2+2在區間[0,+∞)上是增函數.
點評:本題考查了函數單調性的判斷與證明,訓練了因式分解法,解答此題的關鍵是因式分解要徹底,避免出現證題用題的現象的發生.是基礎題.

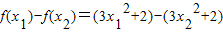
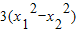 =3(x1+x2)(x1-x2).
=3(x1+x2)(x1-x2).
