Question

18．設m，n∈R，定義在區間[m，n]上函數f（x）=x²的值域是[0，4]，若關于t的方程|3^-|t|-$\frac{1}{4}$|-n=0恰有4個互不相等的實數解，則m+n的取值范圍是$（{-2，-\frac{7}{4}}）$．

Answer 1

分析 畫出函數y=|3^-|t|-$\frac{1}{4}$|的圖象，由關于t的方程|3^-|t|-$\frac{1}{4}$|-n=0恰有4個互不相等的實數解，求出n的范圍，再由定義在區間[m，n]上函數f（x）=x²的值域是[0，4]，求出m值，可得答案．

解答 解：函數y=|3^-|t|-$\frac{1}{4}$|的圖象如下圖所示：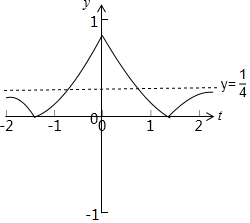

若關于t的方程|3^-|t|-$\frac{1}{4}$|-n=0恰有4個互不相等的實數解，
則n∈（0，$\frac{1}{4}$），
∵定義在區間[m，n]上函數f（x）=x²的值域是[0，4]，
∴m=-2，
故m+n∈$（{-2，-\frac{7}{4}}）$，
故答案為：$（{-2，-\frac{7}{4}}）$

點評 本題考查的知識點是函數的圖象，方程根的個數，數形結合思想，二次函數的圖象和性質，難度中檔．