某公司計劃在甲、乙兩個電視臺做總時間不超過300分鐘的廣告,廣告費用不超過9萬元,甲、乙電視臺的廣告費標準分別是500元/分鐘和200元/分鐘,假設甲、乙兩個電視臺為該公司做的廣告能給公司帶來的收益分別為0.2萬元/分鐘和0.1萬元/分鐘,那么該公司合理分配在甲、乙兩個電視臺的廣告時間,能使公司獲得最大的收益是( )萬元.
A.30
B.36
C.40
D.45
【答案】
分析:利用線性規劃的思想方法解決,先列出約束條件,寫出目標函數,作出可行域,利用圖象,即可得到結論.
解答: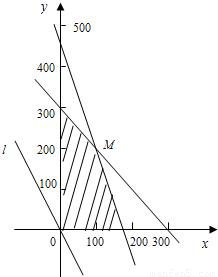
解:設公司在甲電視臺和乙電視臺做廣告的時間分別為x分鐘和y分鐘,總收益為z元,由題意得
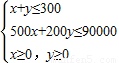
目標函數為z=2000x+1000y.
作出二元一次不等式組所表示的平面區域,即可行域.
如圖,作直線l:3000x+2000y=0,即3x+2y=0.
平移直線l,從圖中可知,當直線l過M點時,目標函數取得最大值.
聯立
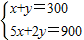
,解得x=100,y=200.
∴點M的坐標為(100,200).
∴z
max=2000x+1000y=400000(元)
故選C.
點評:本題主要考查找出約束條件與目標函數,準確地描畫可行域,再利用圖形直線求得滿足題設的最優解.用圖解法解決線性規劃問題時,分析題目的已知條件,找出約束條件和目標函數是關鍵,可先將題目中的量分類、列出表格,理清頭緒,然后列出不等式組(方程組)尋求約束條件,并就題目所述找出目標函數.然后將可行域各角點的值一一代入,最后比較,即可得到目標函數的最優解.

 解:設公司在甲電視臺和乙電視臺做廣告的時間分別為x分鐘和y分鐘,總收益為z元,由題意得
解:設公司在甲電視臺和乙電視臺做廣告的時間分別為x分鐘和y分鐘,總收益為z元,由題意得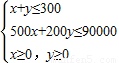
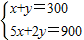 ,解得x=100,y=200.
,解得x=100,y=200.

 名校課堂系列答案
名校課堂系列答案