
分析 (1)f′(x)=ex-a,根據函數f(x)=ex-ax有極值1,可得存在x0,使得f′(x0)=${e}^{{x}_{0}}$-a=0,f(x0)=${e}^{{x}_{0}}$-ax0=1,解得x0,a.即可判斷出結論.
(2)當x∈[0,+∞)時,f(x)≥mxln(x+1)+1恒成立?ex-x-1-mxln(x+1)≥0恒成立.令g(x)=ex-(x+1),x≥0.g(0)=0.利用導數研究其單調性可得:ex≥x+1.
①若mxln(x+1)+x+1≤x+1,則ex-x-1-mxln(x+1)≥0恒成立.可得:m≤0.
②m>0時,x≥0時,mxln(x+1)+x+1≤ex.令F(x)=mxln(x+1)+x+1-ex,(x≥0),F(0)=0.
由F(x)≤0,可得mxln(x+1)≤ex-x-1,x>0時,化為:m≤$\frac{{e}^{x}-x-1}{xln(x+1)}$.下面證明:$\frac{1}{2}$≤$\frac{{e}^{x}-x-1}{xln(x+1)}$.利用導數研究其單調性即可得出.
解答 解:(1)f′(x)=ex-a,∵函數f(x)=ex-ax有極值1,
∴存在x0,使得f′(x0)=${e}^{{x}_{0}}$-a=0,f(x0)=${e}^{{x}_{0}}$-ax0=1,
解得x0=0,a=1.
∴f′(x)=ex-1,可知:0是極小值點,因此1是極小值.
(2)當x∈[0,+∞)時,f(x)≥mxln(x+1)+1恒成立?ex-x-1-mxln(x+1)≥0恒成立.
令g(x)=ex-(x+1),x≥0.g(0)=0.
則g′(x)=ex-1≥0,
∴x≥0時,函數g(x)單調遞增,因此g(x)≥g(0)=0,因此ex≥x+1.
①若mxln(x+1)+x+1≤x+1,則ex-x-1-mxln(x+1)≥0恒成立.
則mxln(x+1)≤0,可得:m≤0.
∴m≤0時,x≥0時,f(x)≥mxln(x+1)+1恒成立.
②m>0時,x≥0時,mxln(x+1)+x+1≤ex.
令F(x)=mxln(x+1)+x+1-ex,(x≥0),F(0)=0.
由F(x)≤0,可得mxln(x+1)≤ex-x-1,
x=0時,化為0≤0,恒成立,m∈R.
x>0時,化為:m≤$\frac{{e}^{x}-x-1}{xln(x+1)}$.
下面證明:$\frac{1}{2}$≤$\frac{{e}^{x}-x-1}{xln(x+1)}$.
令h(x)=2ex-2x-2-xln(x+1),h(0)=0.
h′(x)=2ex-2-ln(x+1)-$\frac{x}{x+1}$.h′(0)=0.
h″(x)=2ex-$\frac{1}{x+1}$-$\frac{1}{(x+1)^{2}}$≥h″(0)=0,
∴h′(x)≥0.
∴函數h(x)在[0,+∞)上單調遞增,∴h(x)≥h(0)=0.
因此:$\frac{1}{2}$≤$\frac{{e}^{x}-x-1}{xln(x+1)}$成立,并且$\frac{1}{2}$是其最小值.
∴m≤$\frac{1}{2}$.
綜上可得:實數m的取值范圍是$(-∞,\frac{1}{2}]$.
點評 本題考查了利用導數研究函數的單調性極值與最值、分類討論方法、方程與不等式的解法、等價轉化方法,考查了推理能力與計算能力,屬于難題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
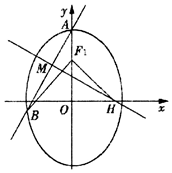 已知橢圓C:$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1({a>b>0})$的上、下焦點分別為F1,F2,上焦點F1到直線 4x+3y+12=0的距離為3,橢圓C的離心率e=$\frac{1}{2}$.
已知橢圓C:$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1({a>b>0})$的上、下焦點分別為F1,F2,上焦點F1到直線 4x+3y+12=0的距離為3,橢圓C的離心率e=$\frac{1}{2}$.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | x2+y2=5 | B. | x2+y2=3 | C. | x2+y2=9 | D. | x2+y2=7 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
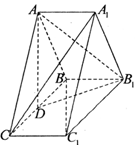 如圖,在三棱柱ABC-A1B1C1中,側棱AA1⊥底面ABC,D為棱BC的中點,AB=AC,BC=$\sqrt{2}A{A_1}$,求證:
如圖,在三棱柱ABC-A1B1C1中,側棱AA1⊥底面ABC,D為棱BC的中點,AB=AC,BC=$\sqrt{2}A{A_1}$,求證:查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1+$\sqrt{6}$ | B. | 1+$\sqrt{5}$ | C. | 1+$\sqrt{3}$ | D. | 1+$\sqrt{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
 將一張邊長為12cm的正方形紙片按如圖(1)所示陰影部分裁去四個全等的等腰三角形,將余下部分沿虛線折疊并拼成一個有底的正四棱錐模型,如圖(2)所示放置.如果正四棱錐的主視圖是等邊三角形,如圖(3)所示,則正四棱錐的體積是( )
將一張邊長為12cm的正方形紙片按如圖(1)所示陰影部分裁去四個全等的等腰三角形,將余下部分沿虛線折疊并拼成一個有底的正四棱錐模型,如圖(2)所示放置.如果正四棱錐的主視圖是等邊三角形,如圖(3)所示,則正四棱錐的體積是( )| A. | $\frac{32}{3}$$\sqrt{6}$cm3 | B. | $\frac{64}{3}$$\sqrt{6}$cm3 | C. | $\frac{32}{3}$$\sqrt{2}$cm3 | D. | $\frac{64}{3}$$\sqrt{2}$cm3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com