【題目】數列
的前
項和為
，
．
（
）證明數列
是等比數列，求出數列的通項公式．
（
）設
，求數列
的前項和
．
（
）數列中是否存在三項，它們可以構成等比數列？若存在，求出一組符合條件的項；若不存在，說明理由．
【答案】（1）
（2）
（3）不存在
【解析】分析：(1)先根據和項與通項關系得
, 再代入化簡
得2，最后根據等比數列定義以及通項公式求數列
的通項公式．(2)由于
，再利用錯位相減法求和
，(3)先）假設存在
，
，
，且
，使得
，
，
成等比數列，化簡利用奇偶分析法得
，與矛盾，因此不存在.
詳解：解：（
）數列的前
項和為
，
，
，
∴
，
兩式相減得：
，即，
∴
，即
，
又當
時，
，得
，
∴數列
是以
為首項，
為公比的等比數列，
∴
，
∴
．
（）由題意，
，
∴
，
，
兩式相減得
．
（
）假設存在，，，且，使得，，成等比數列，則
，
∵
，
，
，
∴
，
∴
，
∵
是奇數，
，
也是奇數，
∴
是奇數，
是奇數，即
故
，因此，與矛盾
故數列
中不存在三項，可以構成等比數列．
步步高達標卷系列答案科目：高中數學 來源： 題型：
【題目】選修4—5:不等式選講
已知函數(x)=|2x-a|+ |x -1|.
（Ⅰ）當a=3時,求不等式(x)≥2的解集；
(Ⅱ)若(x)≥5-x對
恒成立,求實數a的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某大學為調研學生在A，B兩家餐廳用餐的滿意度，從在A，B兩家餐廳都用過餐的學生中隨機抽取了100人，每人分別對這兩家餐廳進行評分，滿分均為60分．
整理評分數據，將分數以
為組距分成
組： 
， 
， 
， 
， 
， 
，得到A餐廳分數的頻率分布直方圖，和B餐廳分數的頻數分布表：
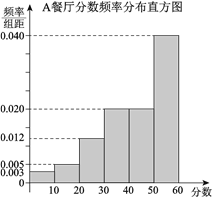
B餐廳分數頻數分布表 | |
分數區間 | 頻數 |
|
|
|
|
|
|
|
|
|
|
|
|
定義學生對餐廳評價的“滿意度指數”如下：
分數 |
|
|
|
滿意度指數 |
|
|
|
（Ⅰ）在抽樣的100人中，求對A餐廳評價“滿意度指數”為
的人數；
（Ⅱ）從該校在A，B兩家餐廳都用過餐的學生中隨機抽取1人進行調查，試估計其對A餐廳評價的“滿意度指數”比對B餐廳評價的“滿意度指數”高的概率；
（Ⅲ）如果從A，B兩家餐廳中選擇一家用餐，你會選擇哪一家？說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】市政府為了節約用水，調查了100位居民某年的月均用水量（單位：
），頻數分布如下：
分組 |
|
|
|
|
|
|
|
|
|
頻數 | 4 | 8 | 15 | 22 | 25 | 14 | 6 | 4 | 2 |
（1）根據所給數據將頻率分布直圖補充完整（不必說明理由）；
（2）根據頻率分布直方圖估計本市居民月均用水量的中位數；
（3）根據頻率分布直方圖估計本市居民月均用水量的平均數（同一組數據由該組區間的中點值作為代表）.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】一牧羊人趕著一群羊通過4個關口，每過一個關口，守關人將拿走當時羊的一半，然后退還一只給牧羊人，過完這些關口后，牧羊人只剩下3只羊，則牧羊人在過第1個關口前有_________只羊.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
