
【題目】某上市公司股票在30天內每股的交易價格P(元)關于時間t(天)的函數關系為 ,該股票在30天內的日交易量Q(萬股)關于時間t(天)的函數為一次函數,其圖象過點
,該股票在30天內的日交易量Q(萬股)關于時間t(天)的函數為一次函數,其圖象過點![]() 和點
和點![]() .
.
(1)求出日交易量Q(萬股)與時間t(天)的一次函數關系式;
(2)用y(萬元)表示該股票日交易額,寫出y關于t的函數關系式,并求在這30天內第幾天日交易額最大,最大值為多少?
 53隨堂測系列答案
53隨堂測系列答案科目:高中數學 來源: 題型:
【題目】已知定直線![]() ,定點
,定點![]() ,以坐標軸為對稱軸的橢圓
,以坐標軸為對稱軸的橢圓![]() 過點
過點![]() 且與
且與![]() 相切.
相切.
(Ⅰ)求橢圓的標準方程;
(Ⅱ)橢圓的弦![]() 的中點分別為
的中點分別為![]() ,若
,若![]() 平行于
平行于![]() ,則
,則![]() 斜率之和是否為定值? 若是定值,請求出該定值;若不是定值請說明理由.
斜率之和是否為定值? 若是定值,請求出該定值;若不是定值請說明理由.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(1)一個袋子中裝有4個大小形狀完全相同的小球,球的編號分別為1,2,3,4,從袋中有放回的取兩個球,設前后兩次取得的球的編號分別為![]() 、
、![]() ,求
,求![]() 的概率;
的概率;
(2)某校早上![]() 開始上課,假設該校學生小張與小王在早上7:30~7:50之間到校,且每人在該時間段內到校時刻是等可能的,求小王比小張至少早5分鐘到校的概率.
開始上課,假設該校學生小張與小王在早上7:30~7:50之間到校,且每人在該時間段內到校時刻是等可能的,求小王比小張至少早5分鐘到校的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】提高過江大橋的車輛通行能力可改善整個城市的交通狀況,在一般情況下,大橋上的車流速度![]() (單位:千米/小時)是車流密度
(單位:千米/小時)是車流密度![]() (單位:輛/千米)的函數.當橋上的車流密度達到
(單位:輛/千米)的函數.當橋上的車流密度達到![]() 輛/千米時,造成堵塞,此時車流速度為
輛/千米時,造成堵塞,此時車流速度為![]() ;當車流密度不超過
;當車流密度不超過![]() 輛/千米時,車流速度為
輛/千米時,車流速度為![]() 千米/小時,研究表明:當
千米/小時,研究表明:當![]() 時,車流速度
時,車流速度![]() 是車流密度
是車流密度![]() 的一次函數.
的一次函數.
(1)當![]() 時,求函數
時,求函數![]() 的表達式;
的表達式;
(2)當車流密度![]() 為多大時,車流量(單位時間內通過橋上某觀測點的車輛數,單位:輛/小時)
為多大時,車流量(單位時間內通過橋上某觀測點的車輛數,單位:輛/小時)![]() 可以達到最大,并求出最大值.
可以達到最大,并求出最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】天水市第一次聯考后,某校對甲、乙兩個文科班的數學考試成績進行分析,
規定:大于或等于120分為優秀,120分以下為非優秀.統計成績后,
得到如下的![]() 列聯表,且已知在甲、乙兩個文科班全部110人中隨機抽取1人為優秀的概率為
列聯表,且已知在甲、乙兩個文科班全部110人中隨機抽取1人為優秀的概率為![]() .
.
優秀 | 非優秀 | 合計 | |
甲班 | 10 | ||
乙班 | 30 | ||
合計 | 110 |
(1)請完成上面的列聯表;
(2)根據列聯表的數據,若按99.9%的可靠性要求,能否認為“成績與班級有關系”;
(3)若按下面的方法從甲班優秀的學生中抽取一人:把甲班優秀的10名學生從2到11進行編號,先后兩次拋擲一枚均勻的骰子,出現的點數之和為被抽取人的序號。試求抽到9號或10號的概率。
參考公式與臨界值表:![]() 。
。
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(2017·石家莊一模)祖暅是南北朝時期的偉大數學家,5世紀末提出體積計算原理,即祖暅原理:“冪勢既同,則積不容異”.意思是:夾在兩個平行平面之間的兩個幾何體,被平行于這兩個平面的任何一個平面所截,如果截面面積都相等,那么這兩個幾何體的體積一定相等.現有以下四個幾何體:圖①是從圓柱中挖去一個圓錐所得的幾何體,圖②、圖③、圖④分別是圓錐、圓臺和半球,則滿足祖暅原理的兩個幾何體為( )
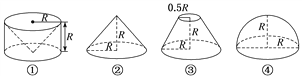
A. ①② B. ①③
C. ②④ D. ①④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】正方體![]() 的棱長為1,
的棱長為1,![]() 分別為
分別為![]() 的中點.有下述四個結論:①直線
的中點.有下述四個結論:①直線![]() 與直線
與直線![]() 垂直;②直線
垂直;②直線![]() 與平面
與平面![]() 平行;③平面
平行;③平面![]() 截正方體所得的截面面積為
截正方體所得的截面面積為![]() ;④直線
;④直線![]() 與直線
與直線![]() 所成角的正切值為
所成角的正切值為![]() ;其中所有正確結論的編號是( )
;其中所有正確結論的編號是( )

A.②③B.②④C.①③D.③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校舉行運動會,其中三級跳遠的成績在8.0米 (四舍五入,精確到0.1米) 以上的進入決賽,把所得數據進行整理后,分成6組畫出頻率分布直方圖的一部分(如圖),已知從左到右前5個小組的頻率分別為0.04,0.10,0.14,0.28,0.30 ,第6小組的頻數是7 .

(Ⅰ)求進入決賽的人數;
(Ⅱ)若從該校學生(人數很多)中隨機抽取兩名,記![]() 表示兩人中進入決賽的人數,求
表示兩人中進入決賽的人數,求![]() 的分布列及數學期望;
的分布列及數學期望;
(Ⅲ) 經過多次測試后發現,甲成績均勻分布在8~10米之間,乙成績均勻分布在9.5~10.5米之間,現甲,乙各跳一次,求甲比乙遠的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() (
(![]() )的焦點F,E上一點
)的焦點F,E上一點![]() 到焦點的距離為4.
到焦點的距離為4.
(1)求拋物線E的方程;
(2)過F作直線l交拋物線E于A,B兩點,若直線AB中點的縱坐標為![]() ,求直線l的方程及弦
,求直線l的方程及弦![]() 的長.
的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com