
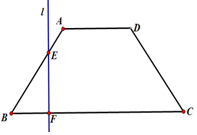
 如圖,已知底角為45°的等腰梯形ABCD,底邊BC長為12,腰長為4$\sqrt{2}$,當一條垂直于底邊BC(垂足為F)的直線l從左至右移動(與梯形ABCD有公共點)時,直線l把梯形分成兩部分.
如圖,已知底角為45°的等腰梯形ABCD,底邊BC長為12,腰長為4$\sqrt{2}$,當一條垂直于底邊BC(垂足為F)的直線l從左至右移動(與梯形ABCD有公共點)時,直線l把梯形分成兩部分.分析 (1)可以通過分類討論明確圖形的特征,再根據圖形形狀求出函數的解析式;
(2)可以求出函數g(x)的解析式,①由解析式即可得到判斷函數的單調性,②分別求出g(3.9)=24.395,g(4.1)=44.84,比較即可.
解答 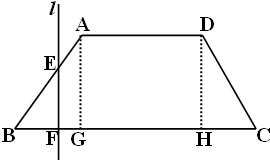 解:(1)過點A.D分別作AG⊥BC,DH⊥BC,垂足分別是G,H.
解:(1)過點A.D分別作AG⊥BC,DH⊥BC,垂足分別是G,H.
∵ABCD是等腰梯形,底角為45°,AB=4$\sqrt{2}$cm,
∴BG=AG=DH=HC=4cm,
又∵BC=12cm,
∴AD=GH=4cm,
①當點F在BG上時,
即x∈(0,4]時,f(x)=32-$\frac{1}{2}$x2;
②當點F在GH上時,
即x∈(4,8]時,f(x)=8+4(8-x)=40-4x.
③當點F在HC上時,
即x∈(8,12)時,y=S五邊形ABFED=S梯形ACD-S三角形CEF
f(x)=$\frac{1}{2}$(12-x)2,
∴函數解析式為f(x)=$\left\{\begin{array}{l}{32-\frac{1}{2}{x}^{2},0<x≤4}\\{40-4x,4<x≤8}\\{\frac{1}{2}(12-x)^{2},8<x<12}\end{array}\right.$,
(2)g(x)=$\left\{\begin{array}{l}{32-\frac{1}{2}{x}^{2},0<x<4}\\{(6-x)(40-4x),4<x<8}\end{array}\right.$,
①由二次函數的性質可知,函數g(x)在(4,8)上是減函數.
②雖然g(x)在(0,4)和(4,8)單調遞減,
但是g(3.9)=24.395,g(4.1)=44.84,
∴g(3.9)<g(4.1).
因此函數g(x)在定義域內不具有單調性.
點評 本題考查了函數的解析式,函數的單調性,屬于中檔題.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-∞,5] | B. | [10,+∞) | C. | (-∞,5]∪[10,+∞) | D. | ∅ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (2,$\sqrt{2}$+1) | B. | ($\sqrt{2}$,$\sqrt{2}$+1) | C. | ($\sqrt{2}$,2) | D. | ($\sqrt{2}$,2)∪(2,$\sqrt{2}$+1) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{\sqrt{3}}{2}$ | B. | 1 | C. | $\frac{\sqrt{5}}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com