
(本小題滿分14分)設函數 .
.
(1)若函數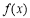 在
在 處有極值,求函數
處有極值,求函數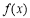 的最大值;
的最大值;
(2)①是否存在實數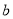 ,使得關于
,使得關于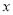 的不等式
的不等式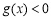 在
在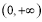 上恒成立?若存在,求出
上恒成立?若存在,求出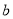 的取值范圍;若不存在,說明理由;
的取值范圍;若不存在,說明理由;
②證明:不等式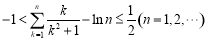 .
.
(1)最大值為 ;(2)①存在,
;(2)①存在,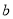 的取值范圍是
的取值范圍是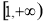 ;②祥見解析.
;②祥見解析.
【解析】
試題分析:(1)由已知得: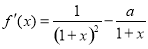 ,且函數f(x)在x=0處有極值,得a=1,從而求出函數的表達式,找出單調區間求出最值;
,且函數f(x)在x=0處有極值,得a=1,從而求出函數的表達式,找出單調區間求出最值;
(2)由已知得: 再對b分情況討論:①若b≥1,②若b≤0,③若0<b<1綜合得出b的取值范圍是x∈[1,+∞);
再對b分情況討論:①若b≥1,②若b≤0,③若0<b<1綜合得出b的取值范圍是x∈[1,+∞);
(3)由前兩問綜合得出.
試題解析:(1)由已知得: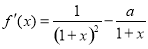 ,且函數
,且函數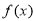 在
在 處有極值
處有極值
∴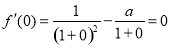 ,即
,即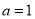
∴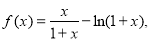 ∴
∴ ,
,
當 時,
時,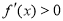 ,
, 單調遞增;
單調遞增;
當 時,
時,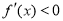 ,
, 單調遞減;
單調遞減;
∴函數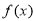 的最大值為
的最大值為
(2)①由已知得:
(i)若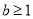 ,則
,則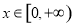 時,
時,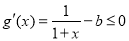
∴ 在
在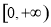 上為減函數,
上為減函數,
∴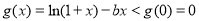 在
在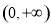 上恒成立;
上恒成立;
(ii)若 ,則
,則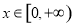 時,
時,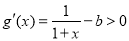
∴ 在
在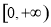 上為增函數,
上為增函數,
∴ ,不能使
,不能使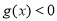 在
在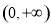 上恒成立;----6分
上恒成立;----6分
(iii)若 ,則
,則 時,
時, ,
,
當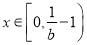 時,
時,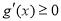 ,∴
,∴ 在
在 上為增函數,
上為增函數,
此時 ,
,
∴不能使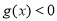 在
在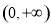 上恒成立;
上恒成立;
綜上所述,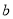 的取值范圍是
的取值范圍是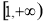
②由以上得: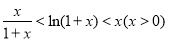 ,取
,取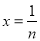 得:
得:

令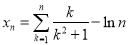 ,
,
則 ,
,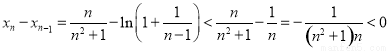 .
.
因此 ;即:
;即: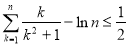 .
.
又
故
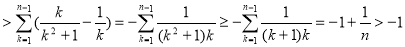
綜上所述:不等式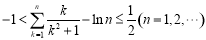 成立
成立
考點:1. 利用導數研究函數的單調性;2. 利用導數求閉區間上函數的最值.


科目:高中數學 來源:2015屆湖北省高三期中考試理科數學試卷(解析版) 題型:選擇題
若函數 ,則下列結論正確的是( )
,則下列結論正確的是( )
A. ,
,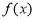 在
在 上是增函數
上是增函數
B. ,
,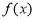 在
在 上是減函數
上是減函數
C.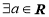 ,
,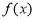 是偶函數
是偶函數
D.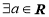 ,
,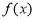 是奇函數
是奇函數
查看答案和解析>>
科目:高中數學 來源:2015屆湖北省高三上學期十月階段性考試理科數學試卷(解析版) 題型:選擇題
已知函數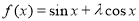 的圖象的一個對稱中心是點
的圖象的一個對稱中心是點 ,則函數
,則函數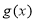 =
= 的圖象的一條對稱軸是直線( )
的圖象的一條對稱軸是直線( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中數學 來源:2015屆湖北省咸寧市高三三校聯考理科數學試卷(解析版) 題型:解答題
(本小題滿分11分)已知函數
(1)求函數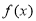 的最小值;
的最小值;
(2)已知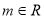 ,命題
,命題 關于
關于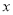 的不等式
的不等式 對任意
對任意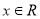 恒成立;命題
恒成立;命題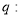 函數
函數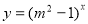 是增函數,若“
是增函數,若“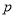 或
或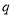 ”為真,“
”為真,“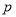 且
且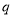 ”為假,求實數
”為假,求實數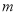 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2015屆湖北省咸寧市高三三校聯考理科數學試卷(解析版) 題型:選擇題
將一圓的六個等分點分成兩組相間的三點﹐它們所構成的兩個正三角形扣除內部六條線段后可以形成一正六角星﹐如圖所示的正六角星是以原點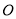 為中心﹐其中
為中心﹐其中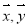 ,分別為原點
,分別為原點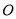 到兩個頂點的向量﹒若將原點
到兩個頂點的向量﹒若將原點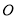 到正六角星12個頂點的向量﹐都寫成為
到正六角星12個頂點的向量﹐都寫成為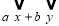 的形式﹐則
的形式﹐則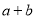 的最大值為( ).
的最大值為( ).

A.2 B.3 C.4 D.5
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com