
分析 (1)根據正弦定理可得和兩角和正弦公式即可求出答案,
(2)根據三角形的面積公式和余弦定理即可求出.
解答 解:(1)∵$\frac{acosB+bcosA}{c}=2cosC$
∴acosB+bcosA=2ccosC,
由正弦定理得:sinAcosB+sinBcosA=2sinCcosC,
即sin(A+B)=2sinCcosC,
∵0<c<π,
∴sinC>0,
∴$cosC=\frac{1}{2}$,
∴$c=\frac{π}{3}$.
(2)由(1)知$C=\frac{π}{3}$,
∵${S_{△ABC}}=2\sqrt{3}$,
∴$\frac{1}{2}$ab×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$b=2$\sqrt{3}$,
解得b=2.
∴${c^2}={a^2}+{b^2}-2ab×\frac{1}{2}=12$,
∴$c=2\sqrt{3}$.
點評 本題考查了正弦定理和余弦定理和三角形的面積公式以及兩角和的正弦公式,考查了學生的運算能力和轉化能力,屬于中檔題.


 名師點撥卷系列答案
名師點撥卷系列答案 英才計劃期末調研系列答案
英才計劃期末調研系列答案科目:高中數學 來源: 題型:選擇題
| A. | 當x=y=a時,數列{an}有最大值$\frac{a}{2}$ | |
| B. | 設bn=an+1-an(n∈N*),則數列{bn}為遞減數列 | |
| C. | 對任意的n∈N*,始終有${a_n}≤\frac{xy}{z}$ | |
| D. | 對任意的n∈N*,都有${a_n}≤\frac{xy}{x+y}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
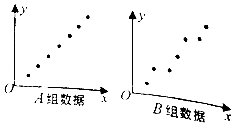 如圖,給出了樣本容量均為7的A、B兩組樣本數據的散點圖,已知A組樣本數據的相關系數為r1,B組數據的相關系數為r2,則( )
如圖,給出了樣本容量均為7的A、B兩組樣本數據的散點圖,已知A組樣本數據的相關系數為r1,B組數據的相關系數為r2,則( )| A. | r1>r2>0 | B. | r2>r1>0 | C. | r1<r2<0 | D. | r2<r1<0 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
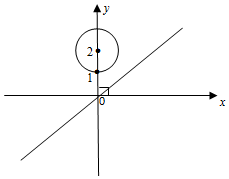 已知圓M的方程為x2+(y-2)2=1,直線l的方程為x-2y=0,點P在直線上,過點P作圓M的切線PA,PB,切點為A,B.
已知圓M的方程為x2+(y-2)2=1,直線l的方程為x-2y=0,點P在直線上,過點P作圓M的切線PA,PB,切點為A,B.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 12 | B. | 18 | C. | 21 | D. | 24 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com