
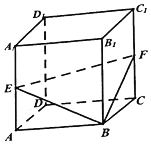
 如圖,在棱長為1的正方體ABCD-A1B1C1D1中,點E,F分別是棱AA1,CC1的中點,P是側面BCC1B1內一點,若A1P∥平面BEF,則線段A1P長度的取值范圍是[$\frac{\sqrt{30}}{5}$,$\sqrt{2}$].
如圖,在棱長為1的正方體ABCD-A1B1C1D1中,點E,F分別是棱AA1,CC1的中點,P是側面BCC1B1內一點,若A1P∥平面BEF,則線段A1P長度的取值范圍是[$\frac{\sqrt{30}}{5}$,$\sqrt{2}$]. 分析 取BB1的中點M,連結A1C1,A1M,C1M,推導出平面BEF∥平面A1MC1,由此得到線段A1P長度的最大值為A1C1=$\sqrt{2}$,最小值為點A1到線段C1M的距離d,從而能求出線段A1P長度的取值范圍.
解答 解: 取BB1的中點M,連結A1C1,A1M,C1M,
取BB1的中點M,連結A1C1,A1M,C1M,
∵在棱長為1的正方體ABCD-A1B1C1D1中,點E,F分別是棱AA1,CC1的中點,
∴BE∥A1M,BF∥C1M,
∵BE∩BF=B,A1M∩C1M=M,BE,BF?平面BEF,A1M,C1M?平面A1MC1,
∴平面BEF∥平面A1MC1,
∵P是側面BCC1B1內一點,A1P∥平面BEF,∴P∈線段C1M,
∵A1C1=$\sqrt{2}$,A1M=C1M=$\frac{\sqrt{5}}{2}$,
∴線段A1P長度的最大值為A1C1=$\sqrt{2}$,最小值為點A1到線段C1M的距離d,
以D為原點,建立空間直角坐標系D-xyz,
則A1(1,0,1),M(1,1,$\frac{1}{2}$),C1=(0,1,1),$\overrightarrow{{C}_{1}{A}_{1}}$=(1,-1,0),$\overrightarrow{{C}_{1}M}$=(1,0,-$\frac{1}{2}$),
∴點A1到線段C1M的距離:
d=|$\overrightarrow{{C}_{1}{A}_{1}}$|$\sqrt{1-[cos<\overrightarrow{{C}_{1}{A}_{1}},\overrightarrow{{C}_{1}M}>]^{2}}$=$\sqrt{2}×\sqrt{1-(\frac{1}{\sqrt{2}•\frac{\sqrt{5}}{2}})^{2}}$=$\frac{\sqrt{30}}{5}$.
∴線段A1P長度的取值范圍是[$\frac{\sqrt{30}}{5}$,$\sqrt{2}$].
故答案為:[$\frac{\sqrt{30}}{5}$,$\sqrt{2}$].
點評 本題考查點、線、面間的距離問題,考查學生的運算能力及推理轉化能力,屬中檔題,解決本題的關鍵是通過構造平行平面尋找P點位置.


科目:高中數學 來源: 題型:選擇題
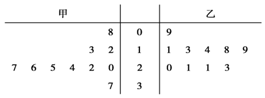 某籃球隊甲、乙兩名運動員練習罰球,每人練習10組,每組罰球40個.命中個數的莖葉圖如圖,則下面結論中錯誤的一個是( )
某籃球隊甲、乙兩名運動員練習罰球,每人練習10組,每組罰球40個.命中個數的莖葉圖如圖,則下面結論中錯誤的一個是( )| A. | 乙的眾數是21 | B. | 甲的中位數是24 | ||
| C. | 甲的極差是29 | D. | 甲罰球命中率比乙高 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (1,$\sqrt{6}$) | B. | (2,$\sqrt{7}$) | C. | (2,$\sqrt{6}$) | D. | (1,$\sqrt{7}$) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 向右平移$\frac{π}{3}$個單位 | B. | 向左平移$\frac{π}{4}$個單位 | ||
| C. | 向左平移$\frac{π}{3}$個單位 | D. | 向右平移$\frac{π}{4}$個單位 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 向左平移$\frac{π}{8}$個單位 | B. | 向左平移$\frac{π}{4}$個單位 | ||
| C. | 向右平移$\frac{π}{8}$個單位 | D. | 向右平移$\frac{π}{4}$個單位 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com