
分析 (x+2y-$\frac{1}{z}$)6展表示6個因式(x+2y-$\frac{1}{z}$)的乘積,故其中1個因式取x,2個因式取2y,剩下的3個因式取-$\frac{1}{z}$,可得展開式中含$\frac{x{y}^{2}}{{z}^{3}}$的項,根據乘法原理求得展開式中$\frac{x{y}^{2}}{{z}^{3}}$的系數.
解答 解:∵(x+2y-$\frac{1}{z}$)6展表示6個因式(x+2y-$\frac{1}{z}$)的乘積,
故其中1個因式取x,2個因式取2y,剩下的3個因式取-$\frac{1}{z}$,
可得展開式中含$\frac{x{y}^{2}}{{z}^{3}}$的項,
故展開式中$\frac{x{y}^{2}}{{z}^{3}}$的系數為${C}_{6}^{1}$•${C}_{5}^{2}$•22•(-1)=-240,
故答案為:-240.
點評 本題主要考查乘方的意義,乘法原理的運用,考查學生的計算能力,比較基礎.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{{y}^{2}}{6}$-$\frac{{x}^{2}}{8}$=1 | B. | $\frac{{y}^{2}}{8}$-$\frac{{y}^{2}}{6}$=1 | C. | $\frac{{x}^{2}}{8}$-$\frac{{y}^{2}}{6}$=1 | D. | $\frac{{x}^{2}}{6}$-$\frac{{y}^{2}}{8}$=1 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 0個 | B. | 1個 | C. | 2個 | D. | 3個 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $-\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | $-\frac{3}{2}$ | D. | -2 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{π}{16}$ | B. | $\frac{π}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
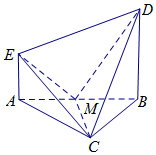 如圖,EA⊥平面ABC,DB⊥平面ABC,△ABC是等邊三角形,AC=2AE,M是AB的中點.
如圖,EA⊥平面ABC,DB⊥平面ABC,△ABC是等邊三角形,AC=2AE,M是AB的中點.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com