
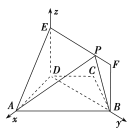
【題目】如圖,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠BCD=120°,四邊形BFED為矩形,平面BFED⊥平面ABCD,BF=1.
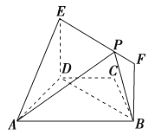
(1)求證:AD⊥平面BFED;
(2)點P在線段EF上運動,設平面PAB與平面ADE所成銳二面角為θ,試求θ的最小值.
【答案】(1)證明見解析 (2)θ最小值為60°
【解析】
(1)在梯形ABCD中,利用勾股定理,得到AD⊥BD,再結合面面垂直的判定,證得DE⊥平面ABCD,即可證得AD⊥平面BFED;
(2)以D為原點,直線DA,DB,DE分別為x軸,y軸,z軸建立如圖所示的空間直角坐標系,求得平面PAB與平面ADE法向量,利用向量的夾角公式,即可求解.
(1)證明:在梯形ABCD中,
∵AB∥CD,AD=DC=CB=1,∠BCD=120°,∴AB=2.
∴BD2=AB2+AD2-2AB·AD·cos 60°=3.
∴AB2=AD2+BD2,∴AD⊥BD.
∵平面BFED⊥平面ABCD,平面BFED∩平面ABCD=BD,
DE平面BFED,DE⊥DB,∴DE⊥平面ABCD,
∴DE⊥AD,又DE∩BD=D,∴AD⊥平面BFED.
(1)由(1)知,直線AD,BD,ED兩兩垂直,故以D為原點,直線DA,DB,DE分別為x軸,y軸,z軸建立如圖所示的空間直角坐標系,
令EP=λ(0≤λ≤![]() ),則D(0,0,0),A(1,0,0),B(0,
),則D(0,0,0),A(1,0,0),B(0,![]() ,0),P(0,λ,1),
,0),P(0,λ,1),
所以![]() =(-1,
=(-1,![]() ,0),
,0),![]() =(0,λ-
=(0,λ-![]() ,1).
,1).
設n1=(x,y,z)為平面PAB的法向量,
由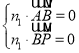 得
得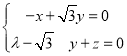 ,取y=1,則n1=(
,取y=1,則n1=(![]() ,1,
,1,![]() -λ).
-λ).
因為n2=(0,1,0)是平面ADE的一個法向量,
所以cos θ=![]() =
=![]() =
=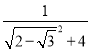 .
.
因為0≤λ≤![]()
![]() 時,cos θ有最大值
時,cos θ有最大值![]() ,所以θ的最小值為60°.
,所以θ的最小值為60°.


科目:高中數學 來源: 題型:
【題目】某班主任對全班50名學生的學習積極性和對待班級工作的態度進行了調查,統計數據如下表所示:
分類 | 積極參加 班級工作 | 不太主動參 加班級工作 | 總計 |
學習積極性高 | 18 | 7 | 25 |
學習積極性一般 | 6 | 19 | 25 |
總計 | 24 | 26 | 50 |
(1)如果隨機抽查這個班的一名學生,那么抽到積極參加班級工作的學生的概率是多少?抽到不太主動參加班級工作且學習積極性一般的學生的概率是多少?
(2)試運用獨立性檢驗的思想方法分析:學生的學習積極性與對待班級工作的態度是否有關,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以原點O為極點,x軸的非負半軸為極軸建立極坐標系,已知曲線C的極坐標方程為![]() (
(![]() ,a為常數)),過點
,a為常數)),過點![]() 、傾斜角為
、傾斜角為![]() 的直線
的直線![]() 的參數方程滿足
的參數方程滿足![]() ,(
,(![]() 為參數).
為參數).
(1)求曲線C的普通方程和直線![]() 的參數方程;
的參數方程;
(2)若直線![]() 與曲線C相交于A、B兩點(點P在A、B之間),且
與曲線C相交于A、B兩點(點P在A、B之間),且![]() ,求
,求![]() 和
和![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國的“洋垃極禁止入境”政策已實施一年多![]() 某沿海地區的海岸線為一段圓弧AB,對應的圓心角
某沿海地區的海岸線為一段圓弧AB,對應的圓心角![]() ,該地區為打擊洋垃圾走私,在海岸線外側20海里內的海域ABCD對不明船只進行識別查證
,該地區為打擊洋垃圾走私,在海岸線外側20海里內的海域ABCD對不明船只進行識別查證![]() 如圖:其中海域與陸地近似看作在同一平面內
如圖:其中海域與陸地近似看作在同一平面內![]() 在圓弧的兩端點A,B分別建有監測站,A與B之間的直線距離為100海里.
在圓弧的兩端點A,B分別建有監測站,A與B之間的直線距離為100海里.
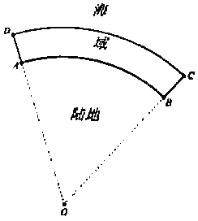
![]() 求海域ABCD的面積;
求海域ABCD的面積;
![]() 現海上P點處有一艘不明船只,在A點測得其距A點40海里,在B點測得其距B點
現海上P點處有一艘不明船只,在A點測得其距A點40海里,在B點測得其距B點![]() 海里
海里![]() 判斷這艘不明船只是否進入了海域ABCD?請說明理由.
判斷這艘不明船只是否進入了海域ABCD?請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知雙曲線![]()
![]() 的兩條漸近線與拋物線
的兩條漸近線與拋物線![]() 的準線分別交于
的準線分別交于![]() ,
,![]() 兩點.若雙曲線
兩點.若雙曲線![]() 的離心率為
的離心率為![]() ,
,![]() 的面積為
的面積為![]() ,
,![]() 為坐標原點,則拋物線
為坐標原點,則拋物線![]() 的焦點坐標為 ( )
的焦點坐標為 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】人造地球衛星繞地球運行遵循開普勒行星運動定律:如圖,衛星在以地球的中心為焦點的橢圓軌道上繞地球運行時,其運行速度是變化的,速度的變化服從面積守恒規律,即衛星的向徑(衛星與地心的連線)在相同的時間內掃過的面積相等設該橢圓的長軸長、焦距分別為![]() ,
,![]() .某同學根據所學知識,得到下列結論:
.某同學根據所學知識,得到下列結論:

①衛星向徑的取值范圍是![]()
②衛星向徑的最小值與最大值的比值越大,橢圓軌道越扁
③衛星在左半橢圓弧的運行時間大于其在右半橢圓弧的運行時間
④衛星運行速度在近地點時最小,在遠地點時最大
其中正確的結論是( )
A.①②B.①③C.②④D.①③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知F1,F2是橢圓與雙曲線的公共焦點,P是它們的一個公共點,且|PF1|<|PF2|,線段PF1的垂直平分線經過點F2,若橢圓的離心率為e1,雙曲線的離心率為e2,則![]() 的最小值為( )
的最小值為( )
A.2B.﹣2C.6D.﹣6
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)討論函數![]() 的單調性;
的單調性;
(2)當![]() 時,若函數
時,若函數![]() 的導函數
的導函數![]() 的圖象與
的圖象與![]() 軸交于
軸交于![]() ,
, ![]() 兩點,其橫坐標分別為
兩點,其橫坐標分別為![]() ,
, ![]() ,線段
,線段![]() 的中點的橫坐標為
的中點的橫坐標為![]() ,且
,且![]() ,
, ![]() 恰為函數
恰為函數![]() 的零點,求證:
的零點,求證: ![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com